Hamiltonian-Driven Shadow Tomography of Quantum States

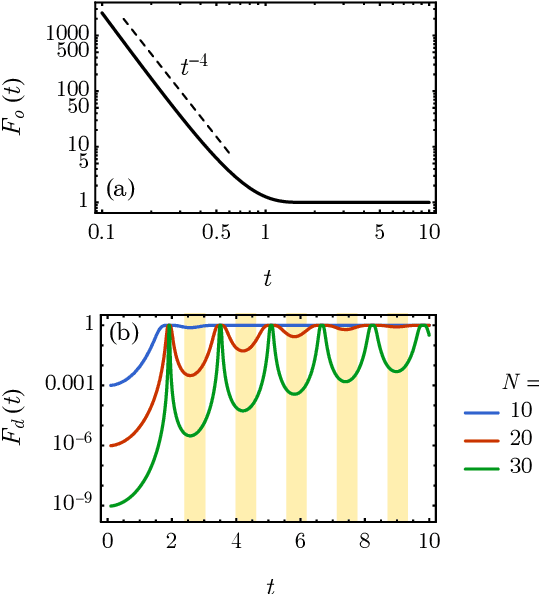
Classical shadow tomography provides an efficient method for predicting functions of an unknown quantum state from a few measurements of the state. It relies on a unitary channel that efficiently scrambles the quantum information of the state to the measurement basis. Facing the challenge of realizing deep unitary circuits on near-term quantum devices, we explore the scenario in which the unitary channel can be shallow and is generated by a quantum chaotic Hamiltonian via time evolution. We provide an unbiased estimator of the density matrix for all ranges of the evolution time. We analyze the sample complexity of the Hamiltonian-driven shadow tomography. We find that it can be more efficient than the unitary-2-design-based shadow tomography in a sequence of intermediate time windows that range from an order-1 scrambling time to a time scale of $D^{1/6}$, given the Hilbert space dimension $D$. In particular, the efficiency of predicting diagonal observables is improved by a factor of $D$ without sacrificing the efficiency of predicting off-diagonal observables.