Group-sparse Matrix Recovery
Paper and Code
Feb 20, 2014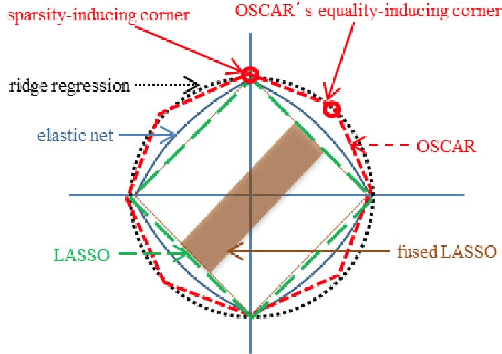
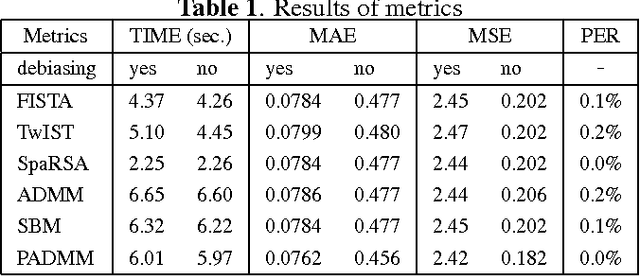
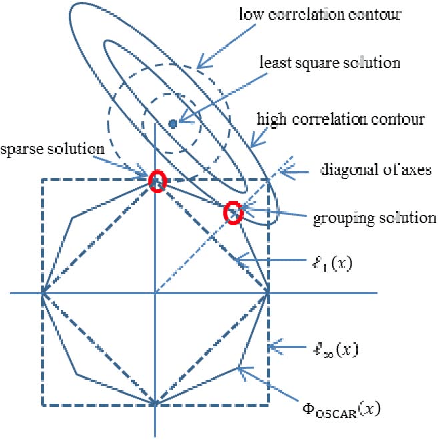

We apply the OSCAR (octagonal selection and clustering algorithms for regression) in recovering group-sparse matrices (two-dimensional---2D---arrays) from compressive measurements. We propose a 2D version of OSCAR (2OSCAR) consisting of the $\ell_1$ norm and the pair-wise $\ell_{\infty}$ norm, which is convex but non-differentiable. We show that the proximity operator of 2OSCAR can be computed based on that of OSCAR. The 2OSCAR problem can thus be efficiently solved by state-of-the-art proximal splitting algorithms. Experiments on group-sparse 2D array recovery show that 2OSCAR regularization solved by the SpaRSA algorithm is the fastest choice, while the PADMM algorithm (with debiasing) yields the most accurate results.
* ICASSP 2014
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge