Group Lasso with Overlaps: the Latent Group Lasso approach
Paper and Code
Oct 03, 2011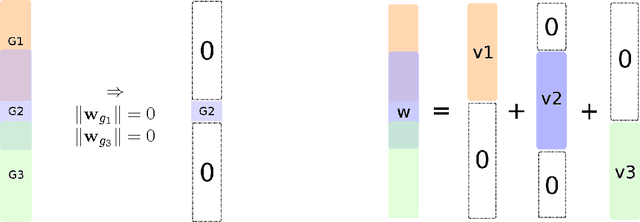

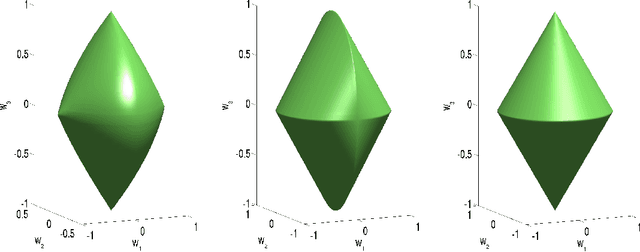

We study a norm for structured sparsity which leads to sparse linear predictors whose supports are unions of prede ned overlapping groups of variables. We call the obtained formulation latent group Lasso, since it is based on applying the usual group Lasso penalty on a set of latent variables. A detailed analysis of the norm and its properties is presented and we characterize conditions under which the set of groups associated with latent variables are correctly identi ed. We motivate and discuss the delicate choice of weights associated to each group, and illustrate this approach on simulated data and on the problem of breast cancer prognosis from gene expression data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge