Greed is Good: Guided Generation from a Greedy Perspective
Paper and Code
Feb 11, 2025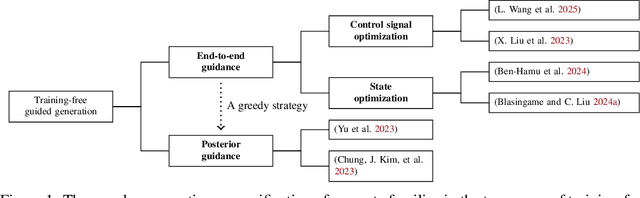
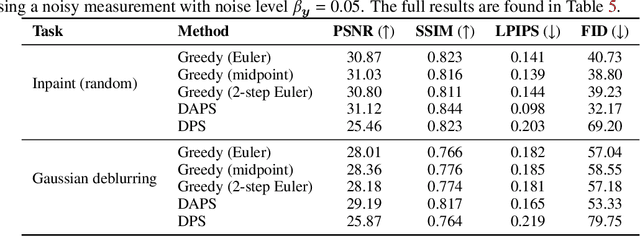
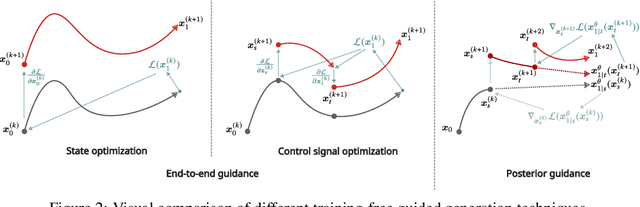
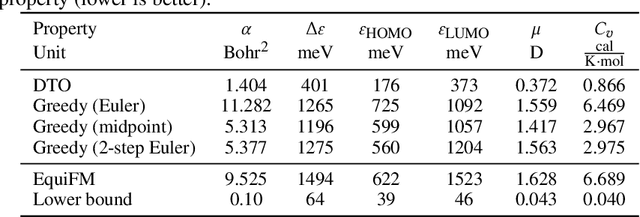
Training-free guided generation is a widely used and powerful technique that allows the end user to exert further control over the generative process of diffusion models. In this work, we explore the guided generation from the perspective of optimizing the solution trajectory of a neural differential equation in a greedy manner. We present such a strategy as a unifying view on training-free guidance by showing that the greedy strategy is a first-order discretization of end-to-end optimization techniques. We show that a greedy guidance strategy makes good decisions and compare it to a guidance strategy using the ideal gradients found via the continuous adjoint equations. We then show how other popular training-free guidance strategies can be viewed in a unified manner from this perspective.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge