Graph2Seq: Scalable Learning Dynamics for Graphs

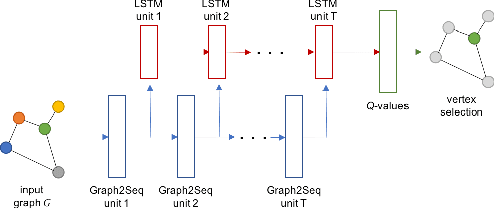
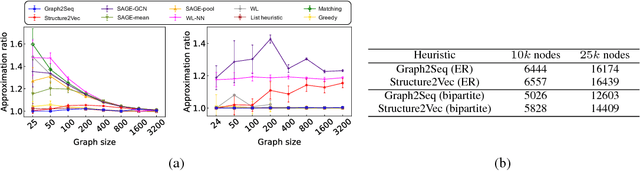
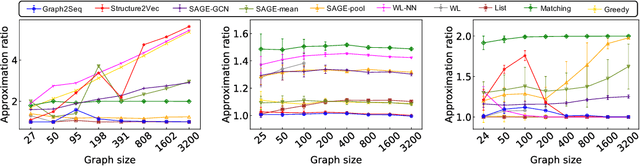
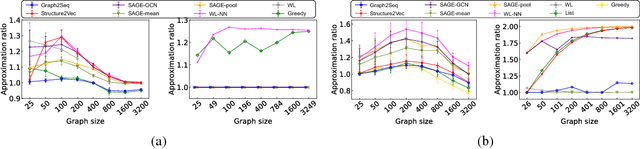
Neural networks have been shown to be an effective tool for learning algorithms over graph-structured data. However, graph representation techniques---that convert graphs to real-valued vectors for use with neural networks---are still in their infancy. Recent works have proposed several approaches (e.g., graph convolutional networks), but these methods have difficulty scaling and generalizing to graphs with different sizes and shapes. We present Graph2Seq, a new technique that represents vertices of graphs as infinite time-series. By not limiting the representation to a fixed dimension, Graph2Seq scales naturally to graphs of arbitrary sizes and shapes. Graph2Seq is also reversible, allowing full recovery of the graph structure from the sequences. By analyzing a formal computational model for graph representation, we show that an unbounded sequence is necessary for scalability. Our experimental results with Graph2Seq show strong generalization and new state-of-the-art performance on a variety of graph combinatorial optimization problems.