Graph Signal Sampling Under Stochastic Priors

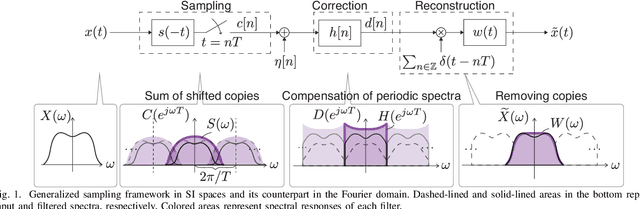
We propose a generalized sampling framework for stochastic graph signals. Stochastic graph signals are characterized by graph wide sense stationarity (GWSS) which is an extension of wide sense stationarity (WSS) for standard time-domain signals. In this paper, graph signals are assumed to satisfy the GWSS conditions and we study their sampling as well as recovery procedures. In generalized sampling, a correction filter is inserted between sampling and reconstruction operators to compensate for non-ideal measurements. We propose a design method for the correction filters to reduce the mean-squared error (MSE) between original and reconstructed graph signals. We derive the correction filters for two cases: The reconstruction filter is arbitrarily chosen or predefined. The proposed framework allows for arbitrary sampling methods, i.e., sampling in the vertex or graph frequency domain. We also show that the graph spectral response of the resulting correction filter parallels that for generalized sampling for WSS signals if sampling is performed in the graph frequency domain. The effectiveness of our approach is validated via experiments by comparing its MSE with existing approaches.