Graph Signal Processing over Multilayer Networks -- Part II: Useful Tools and Practical Applications

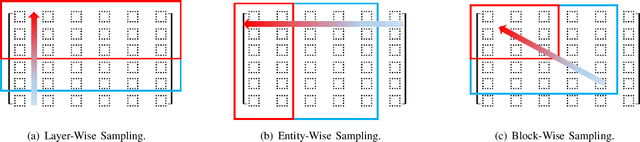
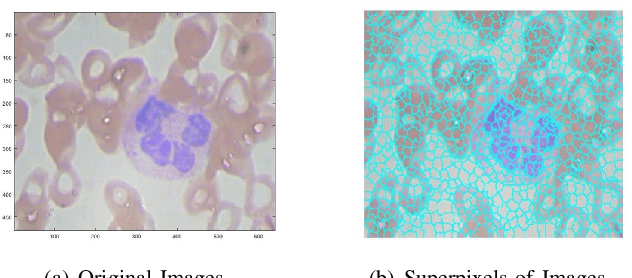
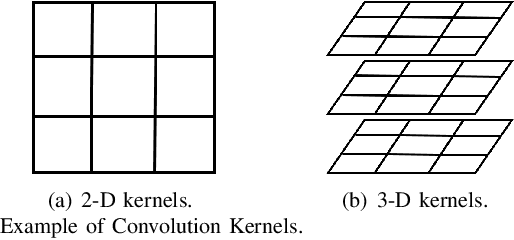
This work introduces a tensor-based framework of graph signal processing over multilayer networks (M-GSP) to analyze high-dimensional signal interactions. Following Part I's introduction of fundamental definitions and spectrum properties of M-GSP, this second Part focuses on more detailed discussions of implementation and applications of M-GSP. Specifically, we define the concepts of stationary process, convolution, bandlimited signals, and sampling theory over multilayer networks. We also develop fundamentals of filter design and derive approximated methods of spectrum estimation within the proposed framework. For practical applications, we further present several MLN-based methods for signal processing and data analysis. Our experimental results demonstrate significant performance improvement using our M-GSP framework over traditional signal processing solutions.