Graph Networks with Spectral Message Passing
Paper and Code
Dec 31, 2020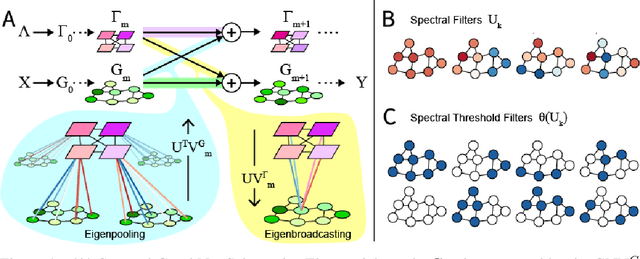
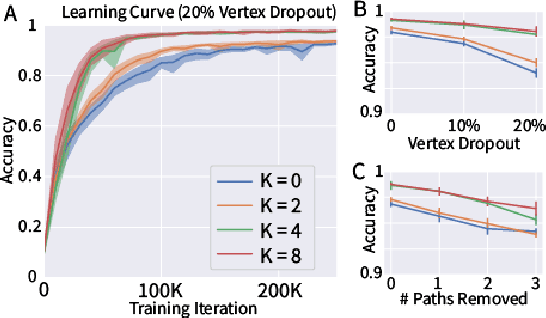
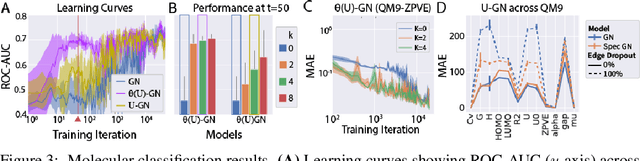
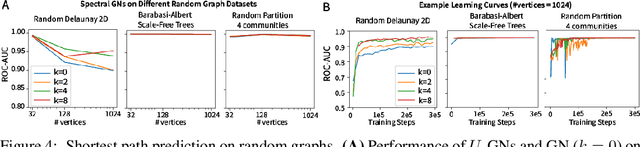
Graph Neural Networks (GNNs) are the subject of intense focus by the machine learning community for problems involving relational reasoning. GNNs can be broadly divided into spatial and spectral approaches. Spatial approaches use a form of learned message-passing, in which interactions among vertices are computed locally, and information propagates over longer distances on the graph with greater numbers of message-passing steps. Spectral approaches use eigendecompositions of the graph Laplacian to produce a generalization of spatial convolutions to graph structured data which access information over short and long time scales simultaneously. Here we introduce the Spectral Graph Network, which applies message passing to both the spatial and spectral domains. Our model projects vertices of the spatial graph onto the Laplacian eigenvectors, which are each represented as vertices in a fully connected "spectral graph", and then applies learned message passing to them. We apply this model to various benchmark tasks including a graph-based variant of MNIST classification, molecular property prediction on MoleculeNet and QM9, and shortest path problems on random graphs. Our results show that the Spectral GN promotes efficient training, reaching high performance with fewer training iterations despite having more parameters. The model also provides robustness to edge dropout and outperforms baselines for the classification tasks. We also explore how these performance benefits depend on properties of the dataset.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge