Graph Encoder Embedding

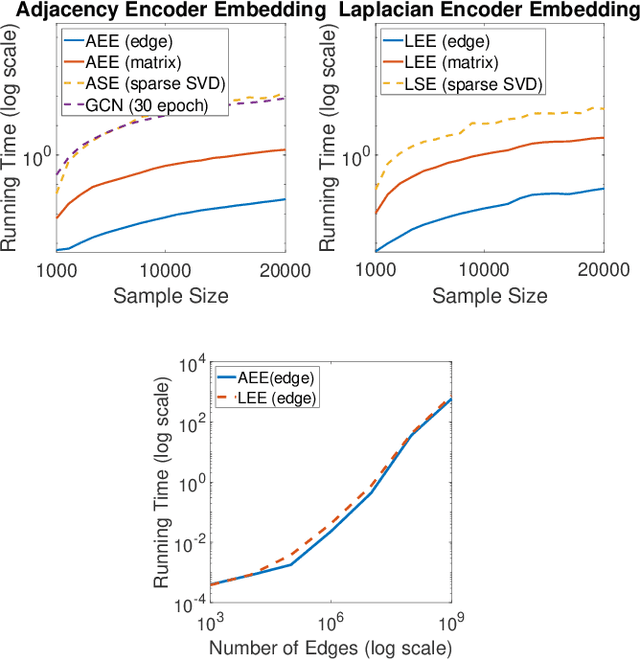
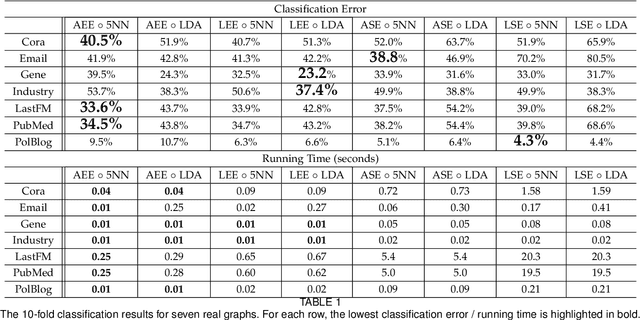
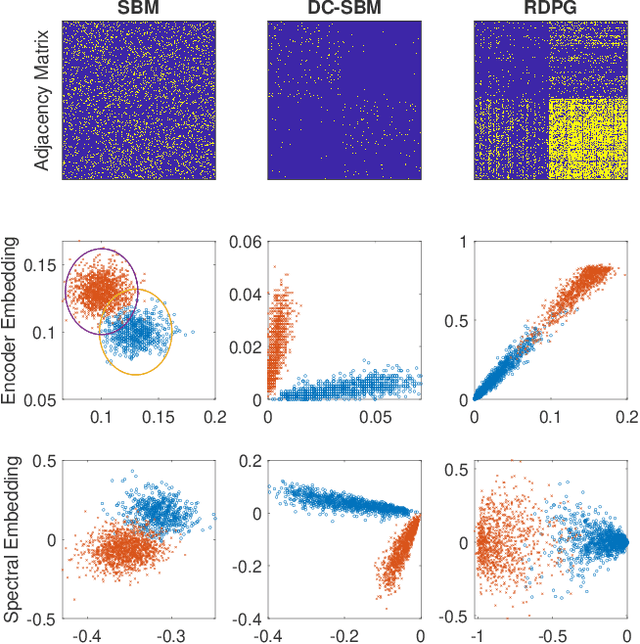
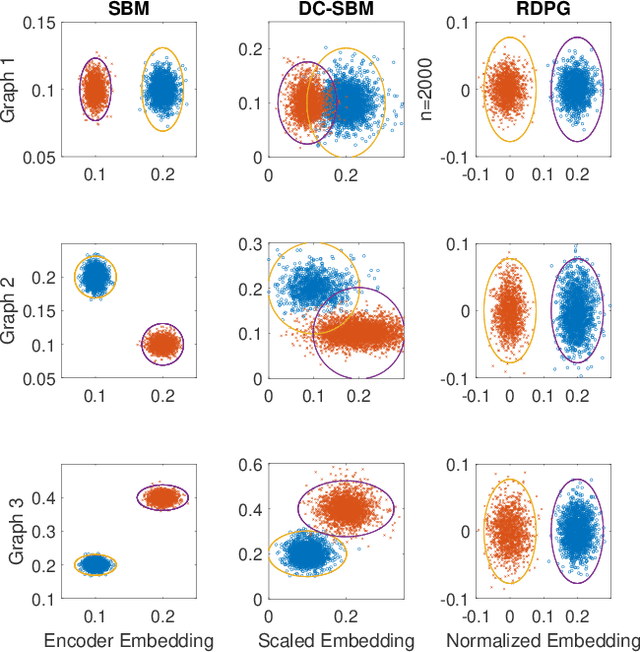
In this paper we propose a lightning fast graph embedding method called graph encoder embedding. The proposed method has a linear computational complexity and the capacity to process billions of edges within minutes on standard PC -- an unattainable feat for any existing graph embedding method. The speedup is achieved without sacrificing embedding performance: the encoder embedding performs as good as, and can be viewed as a transformation of the more costly spectral embedding. The encoder embedding is applicable to either adjacency matrix or graph Laplacian, and is theoretically sound, i.e., under stochastic block model or random dot product graph, the graph encoder embedding asymptotically converges to the block probability or latent positions, and is approximately normally distributed. We showcase three important applications: vertex classification, vertex clustering, and graph bootstrap; and the embedding performance is evaluated via a comprehensive set of synthetic and real data. In every case, the graph encoder embedding exhibits unrivalled computational advantages while delivering excellent numerical performance.