Graph Embedding via High Dimensional Model Representation for Hyperspectral Images
Paper and Code
Nov 29, 2021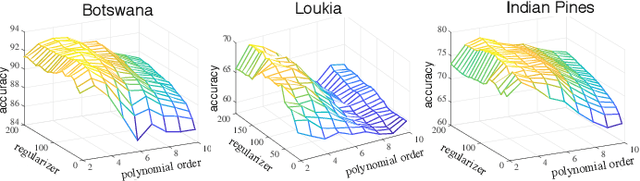
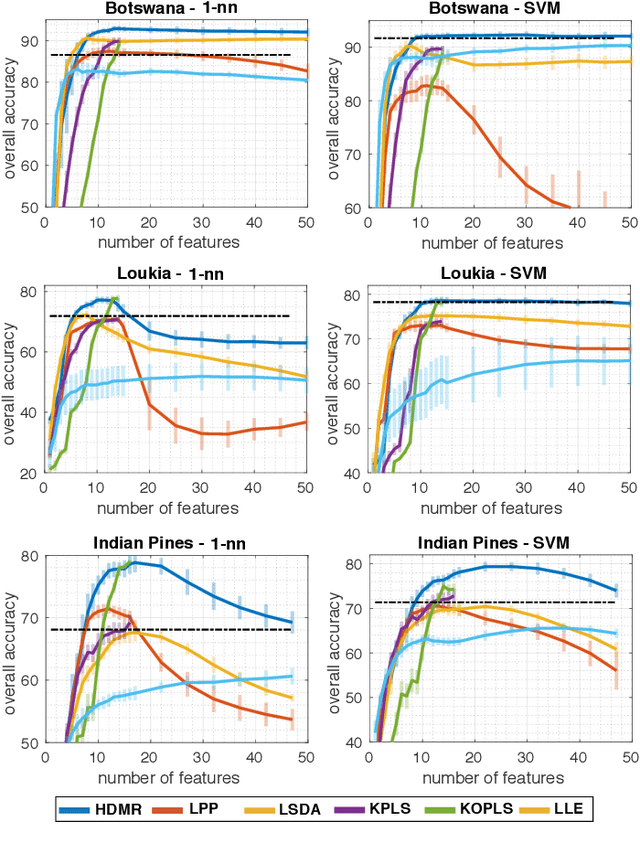
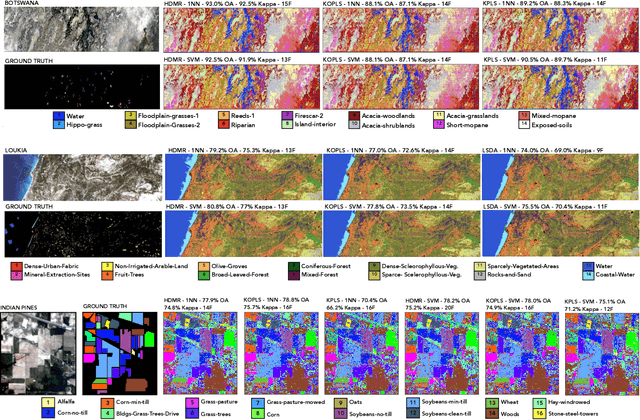
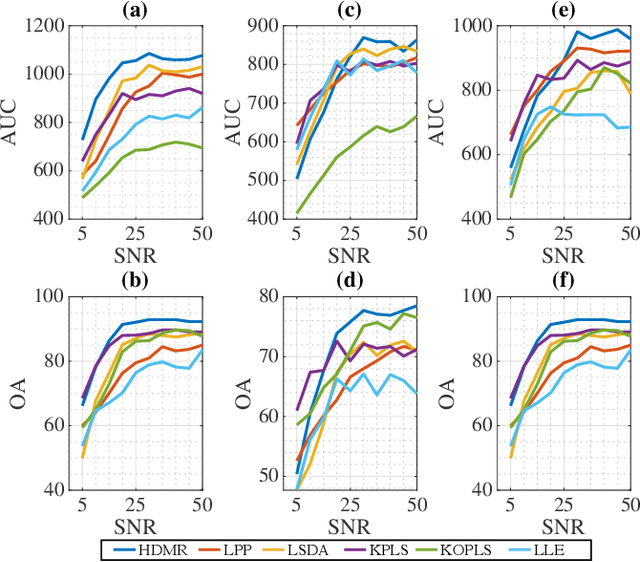
Learning the manifold structure of remote sensing images is of paramount relevance for modeling and understanding processes, as well as to encapsulate the high dimensionality in a reduced set of informative features for subsequent classification, regression, or unmixing. Manifold learning methods have shown excellent performance to deal with hyperspectral image (HSI) analysis but, unless specifically designed, they cannot provide an explicit embedding map readily applicable to out-of-sample data. A common assumption to deal with the problem is that the transformation between the high-dimensional input space and the (typically low) latent space is linear. This is a particularly strong assumption, especially when dealing with hyperspectral images due to the well-known nonlinear nature of the data. To address this problem, a manifold learning method based on High Dimensional Model Representation (HDMR) is proposed, which enables to present a nonlinear embedding function to project out-of-sample samples into the latent space. The proposed method is compared to manifold learning methods along with its linear counterparts and achieves promising performance in terms of classification accuracy of a representative set of hyperspectral images.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge