Grammar Equations
Paper and Code
Jun 14, 2021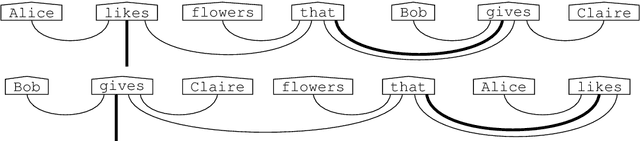
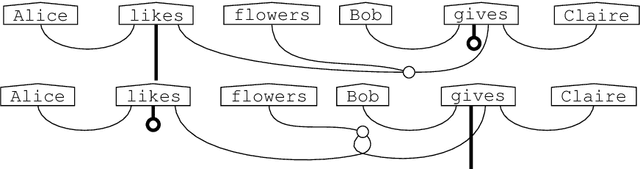
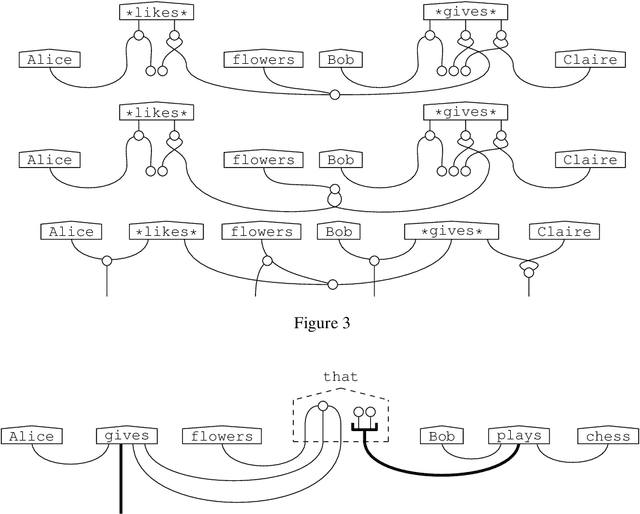
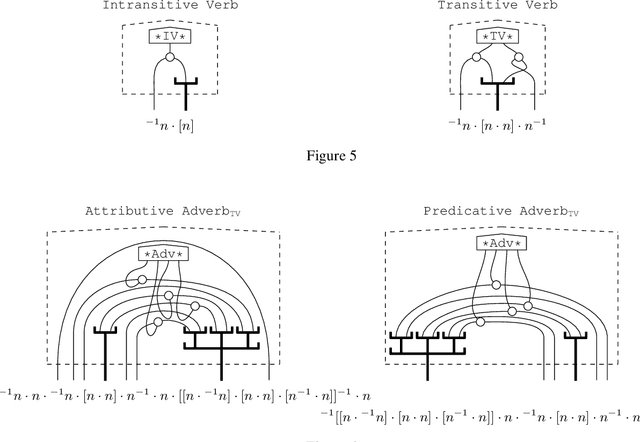
Diagrammatically speaking, grammatical calculi such as pregroups provide wires between words in order to elucidate their interactions, and this enables one to verify grammatical correctness of phrases and sentences. In this paper we also provide wirings within words. This will enable us to identify grammatical constructs that we expect to be either equal or closely related. Hence, our work paves the way for a new theory of grammar, that provides novel `grammatical truths'. We give a nogo-theorem for the fact that our wirings for words make no sense for preordered monoids, the form which grammatical calculi usually take. Instead, they require diagrams -- or equivalently, (free) monoidal categories.
* 10 pages, many pictures
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge