Good linear classifiers are abundant in the interpolating regime

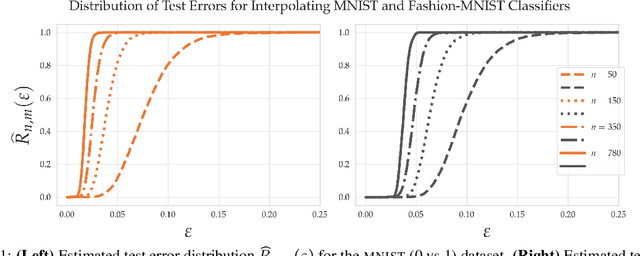
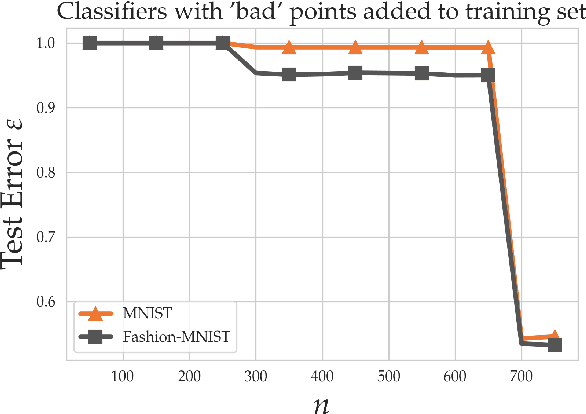
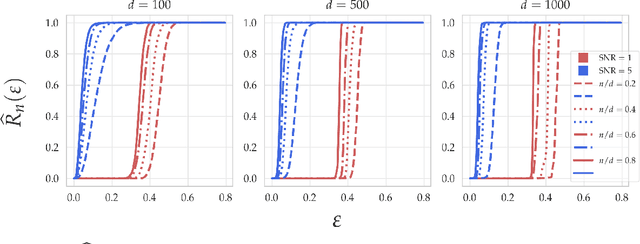
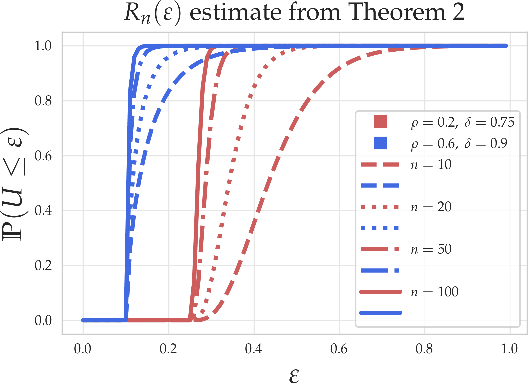
Within the machine learning community, the widely-used uniform convergence framework seeks to answer the question of how complex models such as modern neural networks can generalize well to new data. This approach bounds the test error of the \emph{worst-case} model one could have fit to the data, which presents fundamental limitations. In this paper, we revisit the statistical mechanics approach to learning, which instead attempts to understand the behavior of the \emph{typical} model. To quantify this typicality in the setting of over-parameterized linear classification, we develop a methodology to compute the full distribution of test errors among interpolating classifiers. We apply our method to compute this distribution for several real and synthetic datasets. We find that in many regimes of interest, an overwhelming proportion of interpolating classifiers have good test performance, even though---as we demonstrate---classifiers with very high test error do exist. This shows that the behavior of the worst-case model can deviate substantially from that of the usual model. Furthermore, we observe that for a given training set and testing distribution, there is a critical value $\varepsilon^* > 0$ which is \emph{typical}, in the sense that nearly all test errors eventually concentrate around it. Based on these empirical results, we study this phenomenon theoretically under simplifying assumptions on the data, and we derive simple asymptotic expressions for both the distribution of test errors as well as the critical value $\varepsilon^*$. Both of these results qualitatively reproduce our empirical findings. Our results show that the usual style of analysis in statistical learning theory may not be fine-grained enough to capture the good generalization performance observed in practice, and that approaches based on the statistical mechanics of learning offer a promising alternative.