Global Weighted Tensor Nuclear Norm for Tensor Robust Principal Component Analysis
Paper and Code
Sep 28, 2022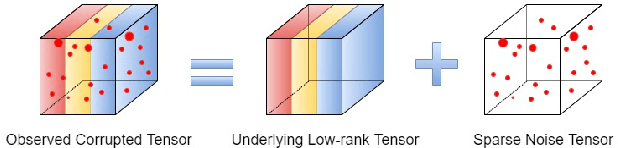
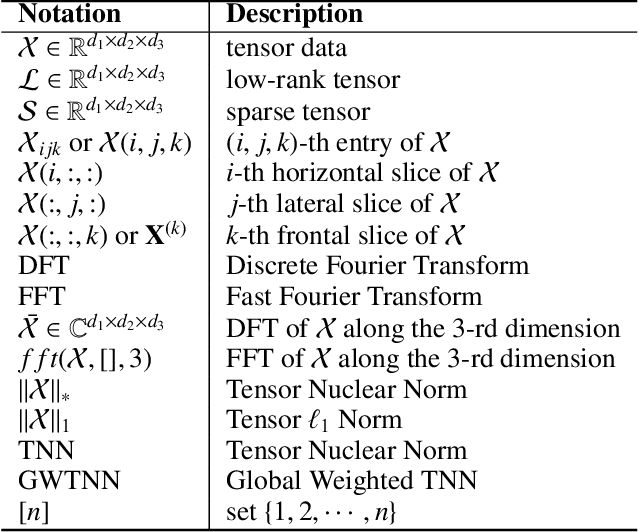
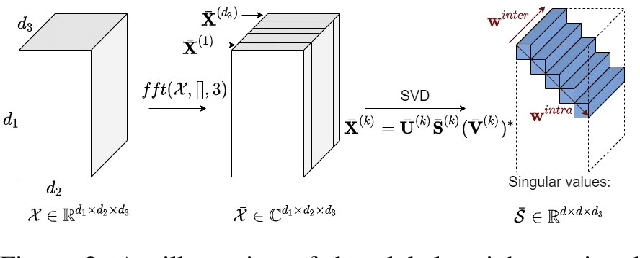
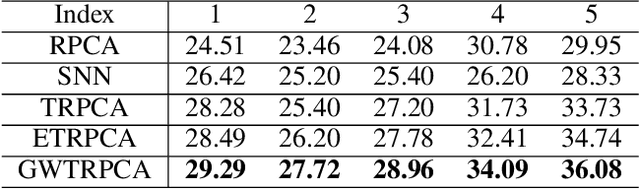
Tensor Robust Principal Component Analysis (TRPCA), which aims to recover a low-rank tensor corrupted by sparse noise, has attracted much attention in many real applications. This paper develops a new Global Weighted TRPCA method (GWTRPCA), which is the first approach simultaneously considers the significance of intra-frontal slice and inter-frontal slice singular values in the Fourier domain. Exploiting this global information, GWTRPCA penalizes the larger singular values less and assigns smaller weights to them. Hence, our method can recover the low-tubal-rank components more exactly. Moreover, we propose an effective adaptive weight learning strategy by a Modified Cauchy Estimator (MCE) since the weight setting plays a crucial role in the success of GWTRPCA. To implement the GWTRPCA method, we devise an optimization algorithm using an Alternating Direction Method of Multipliers (ADMM) method. Experiments on real-world datasets validate the effectiveness of our proposed method.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge