Global Convergence of MAML and Theory-Inspired Neural Architecture Search for Few-Shot Learning

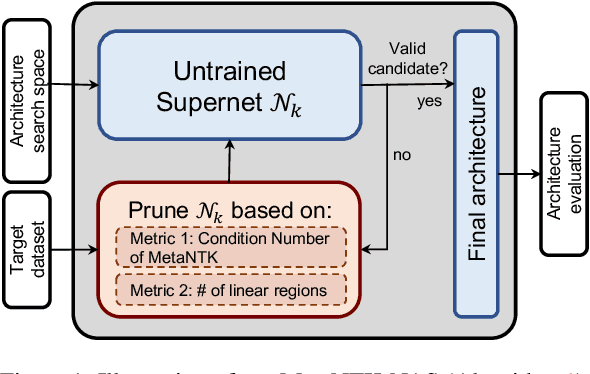
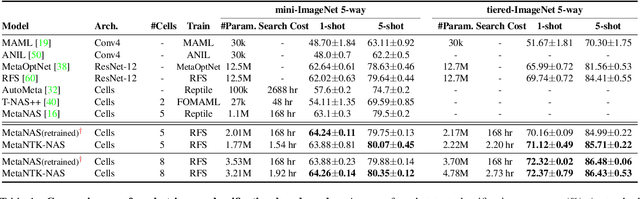
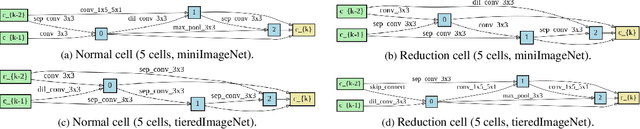
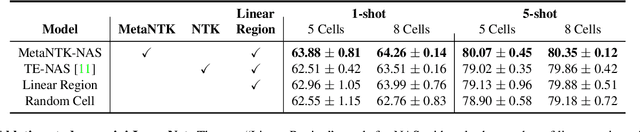
Model-agnostic meta-learning (MAML) and its variants have become popular approaches for few-shot learning. However, due to the non-convexity of deep neural nets (DNNs) and the bi-level formulation of MAML, the theoretical properties of MAML with DNNs remain largely unknown. In this paper, we first prove that MAML with over-parameterized DNNs is guaranteed to converge to global optima at a linear rate. Our convergence analysis indicates that MAML with over-parameterized DNNs is equivalent to kernel regression with a novel class of kernels, which we name as Meta Neural Tangent Kernels (MetaNTK). Then, we propose MetaNTK-NAS, a new training-free neural architecture search (NAS) method for few-shot learning that uses MetaNTK to rank and select architectures. Empirically, we compare our MetaNTK-NAS with previous NAS methods on two popular few-shot learning benchmarks, miniImageNet, and tieredImageNet. We show that the performance of MetaNTK-NAS is comparable or better than the state-of-the-art NAS method designed for few-shot learning while enjoying more than 100x speedup. We believe the efficiency of MetaNTK-NAS makes itself more practical for many real-world tasks.