Global Bandits
Paper and Code
Mar 21, 2018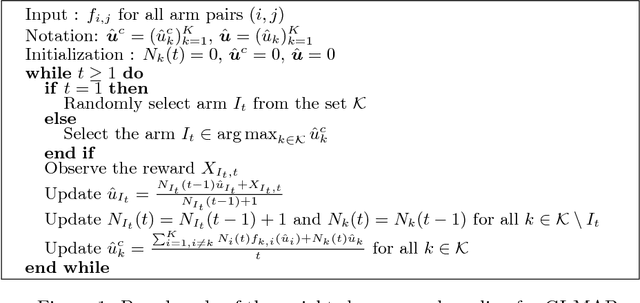

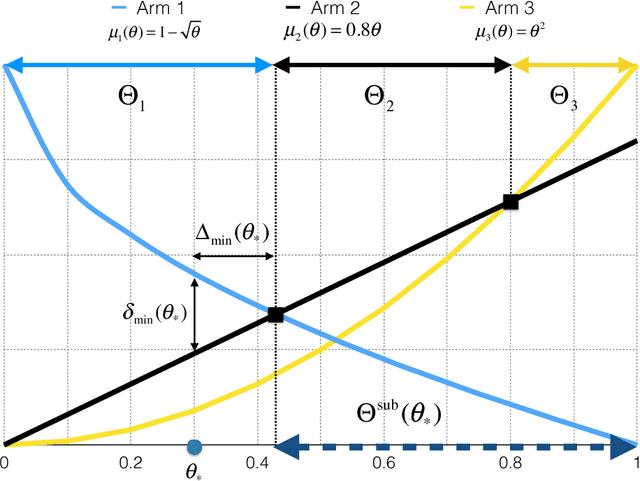
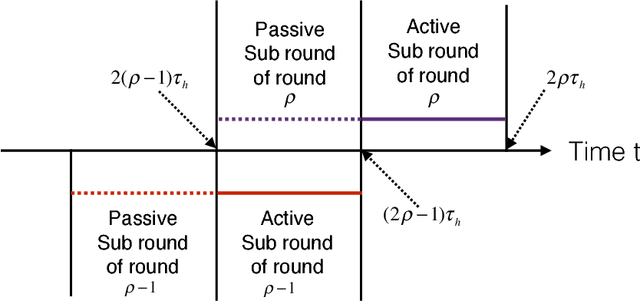
Multi-armed bandits (MAB) model sequential decision making problems, in which a learner sequentially chooses arms with unknown reward distributions in order to maximize its cumulative reward. Most of the prior work on MAB assumes that the reward distributions of each arm are independent. But in a wide variety of decision problems -- from drug dosage to dynamic pricing -- the expected rewards of different arms are correlated, so that selecting one arm provides information about the expected rewards of other arms as well. We propose and analyze a class of models of such decision problems, which we call {\em global bandits}. In the case in which rewards of all arms are deterministic functions of a single unknown parameter, we construct a greedy policy that achieves {\em bounded regret}, with a bound that depends on the single true parameter of the problem. Hence, this policy selects suboptimal arms only finitely many times with probability one. For this case we also obtain a bound on regret that is {\em independent of the true parameter}; this bound is sub-linear, with an exponent that depends on the informativeness of the arms. We also propose a variant of the greedy policy that achieves $\tilde{\mathcal{O}}(\sqrt{T})$ worst-case and $\mathcal{O}(1)$ parameter dependent regret. Finally, we perform experiments on dynamic pricing and show that the proposed algorithms achieve significant gains with respect to the well-known benchmarks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge