GINN-LP: A Growing Interpretable Neural Network for Discovering Multivariate Laurent Polynomial Equations
Paper and Code
Dec 18, 2023
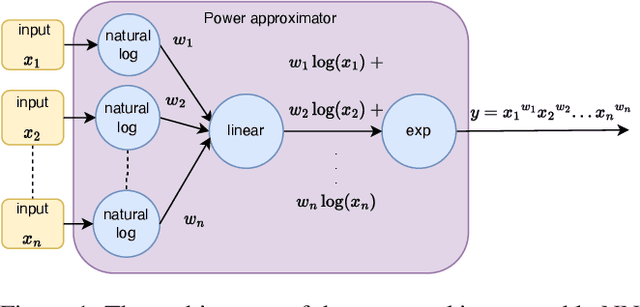

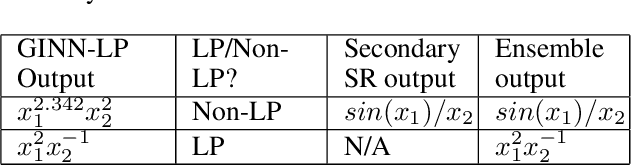
Traditional machine learning is generally treated as a black-box optimization problem and does not typically produce interpretable functions that connect inputs and outputs. However, the ability to discover such interpretable functions is desirable. In this work, we propose GINN-LP, an interpretable neural network to discover the form and coefficients of the underlying equation of a dataset, when the equation is assumed to take the form of a multivariate Laurent Polynomial. This is facilitated by a new type of interpretable neural network block, named the "power-term approximator block", consisting of logarithmic and exponential activation functions. GINN-LP is end-to-end differentiable, making it possible to use backpropagation for training. We propose a neural network growth strategy that will enable finding the suitable number of terms in the Laurent polynomial that represents the data, along with sparsity regularization to promote the discovery of concise equations. To the best of our knowledge, this is the first model that can discover arbitrary multivariate Laurent polynomial terms without any prior information on the order. Our approach is first evaluated on a subset of data used in SRBench, a benchmark for symbolic regression. We first show that GINN-LP outperforms the state-of-the-art symbolic regression methods on datasets generated using 48 real-world equations in the form of multivariate Laurent polynomials. Next, we propose an ensemble method that combines our method with a high-performing symbolic regression method, enabling us to discover non-Laurent polynomial equations. We achieve state-of-the-art results in equation discovery, showing an absolute improvement of 7.1% over the best contender, by applying this ensemble method to 113 datasets within SRBench with known ground-truth equations.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge