Geometric Polynomial Constraints in Higher-Order Graph Matching
Paper and Code
May 24, 2014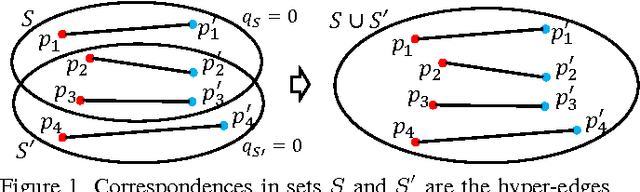
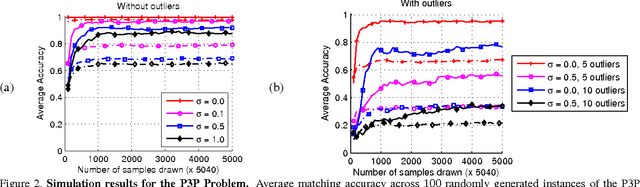
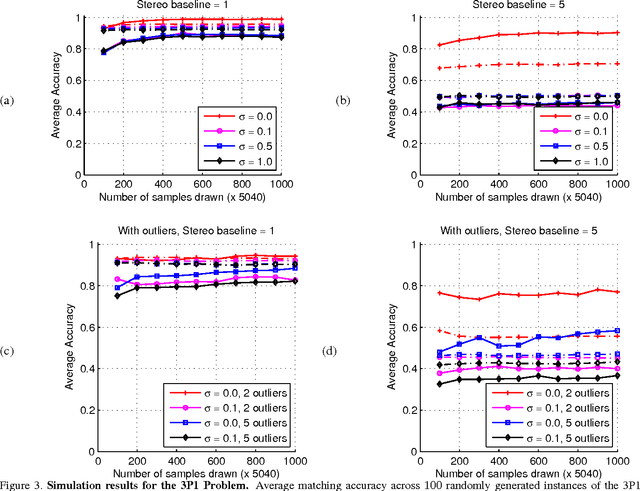
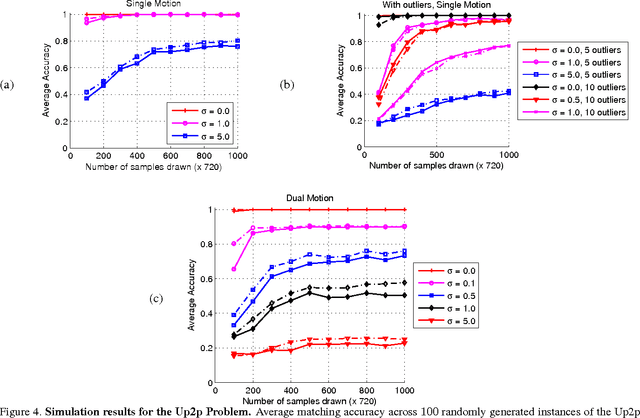
Correspondence is a ubiquitous problem in computer vision and graph matching has been a natural way to formalize correspondence as an optimization problem. Recently, graph matching solvers have included higher-order terms representing affinities beyond the unary and pairwise level. Such higher-order terms have a particular appeal for geometric constraints that include three or more correspondences like the PnP 2D-3D pose problems. In this paper, we address the problem of finding correspondences in the absence of unary or pairwise constraints as it emerges in problems where unary appearance similarity like SIFT matches is not available. Current higher order matching approaches have targeted problems where higher order affinity can simply be formulated as a difference of invariances such as lengths, angles, or cross-ratios. In this paper, we present a method of how to apply geometric constraints modeled as polynomial equation systems. As opposed to RANSAC where such systems have to be solved and then tested for inlier hypotheses, our constraints are derived as a single affinity weight based on $n>2$ hypothesized correspondences without solving the polynomial system. Since the result is directly a correspondence without a transformation model, our approach supports correspondence matching in the presence of multiple geometric transforms like articulated motions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge