Geometric Learning and Topological Inference with Biobotic Networks: Convergence Analysis
Paper and Code
Jun 30, 2016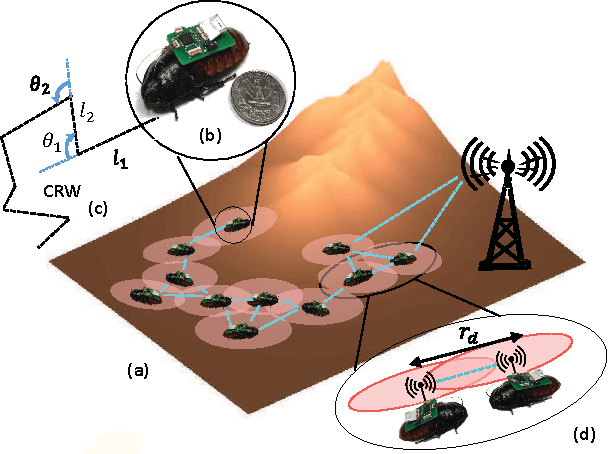
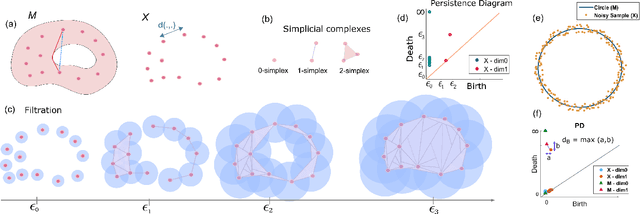
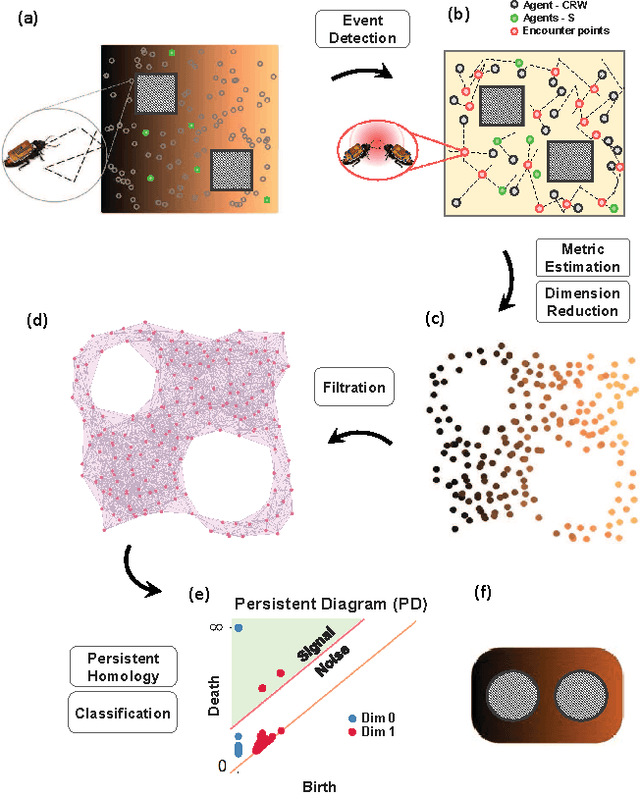
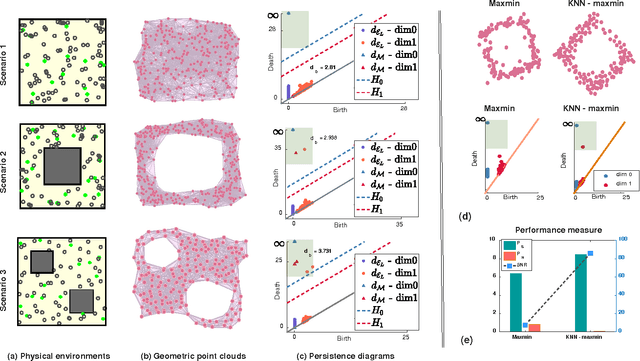
In this study, we present and analyze a framework for geometric and topological estimation for mapping of unknown environments. We consider agents mimicking motion behaviors of cyborg insects, known as biobots, and exploit coordinate-free local interactions among them to infer geometric and topological information about the environment, under minimal sensing and localization constraints. Local interactions are used to create a graphical representation referred to as the encounter graph. A metric is estimated over the encounter graph of the agents in order to construct a geometric point cloud using manifold learning techniques. Topological data analysis (TDA), in particular persistent homology, is used in order to extract topological features of the space and a classification method is proposed to infer robust features of interest (e.g. existence of obstacles). We examine the asymptotic behavior of the proposed metric in terms of the convergence to the geodesic distances in the underlying manifold of the domain, and provide stability analysis results for the topological persistence. The proposed framework and its convergences and stability analysis are demonstrated through numerical simulations and experiments.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge