Generic Axiomatization of Families of Noncrossing Graphs in Dependency Parsing
Paper and Code
Jun 11, 2017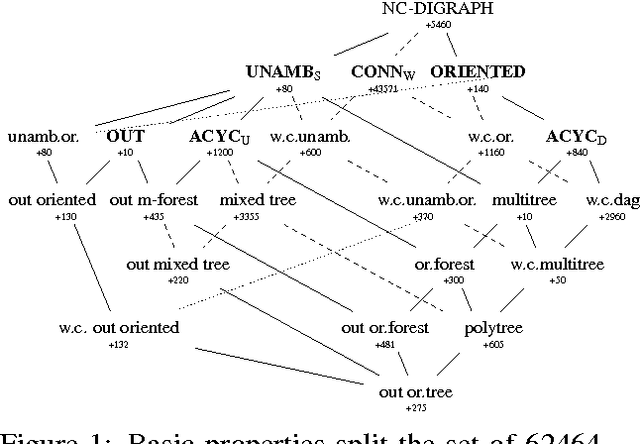


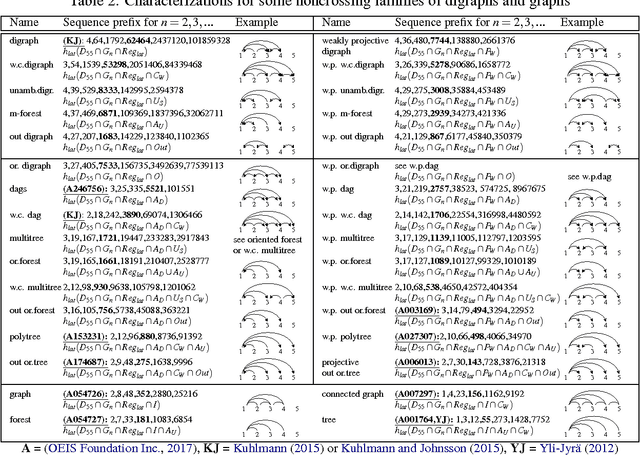
We present a simple encoding for unlabeled noncrossing graphs and show how its latent counterpart helps us to represent several families of directed and undirected graphs used in syntactic and semantic parsing of natural language as context-free languages. The families are separated purely on the basis of forbidden patterns in latent encoding, eliminating the need to differentiate the families of non-crossing graphs in inference algorithms: one algorithm works for all when the search space can be controlled in parser input.
* 11 pages. Accepted for publication at ACL 2017
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge