Generative Flow Networks: a Markov Chain Perspective
Paper and Code
Jul 04, 2023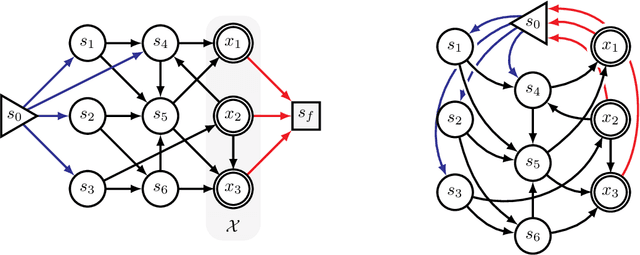

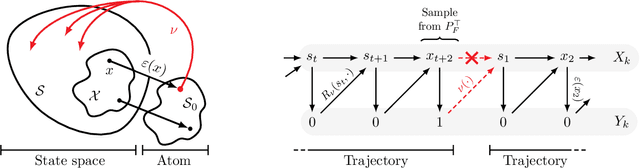
While Markov chain Monte Carlo methods (MCMC) provide a general framework to sample from a probability distribution defined up to normalization, they often suffer from slow convergence to the target distribution when the latter is highly multi-modal. Recently, Generative Flow Networks (GFlowNets) have been proposed as an alternative framework to mitigate this issue when samples have a clear compositional structure, by treating sampling as a sequential decision making problem. Although they were initially introduced from the perspective of flow networks, the recent advances of GFlowNets draw more and more inspiration from the Markov chain literature, bypassing completely the need for flows. In this paper, we formalize this connection and offer a new perspective for GFlowNets using Markov chains, showing a unifying view for GFlowNets regardless of the nature of the state space as recurrent Markov chains. Positioning GFlowNets under the same theoretical framework as MCMC methods also allows us to identify the similarities between both frameworks, and most importantly to highlight their
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge