Generalizing to Unseen Domains with Wasserstein Distributional Robustness under Limited Source Knowledge

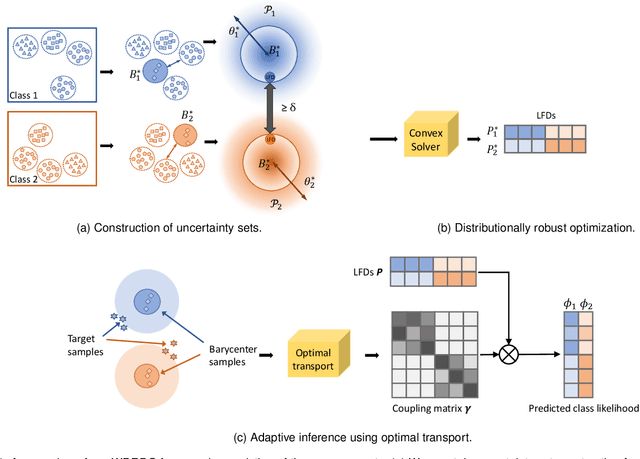
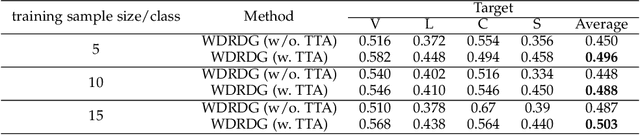
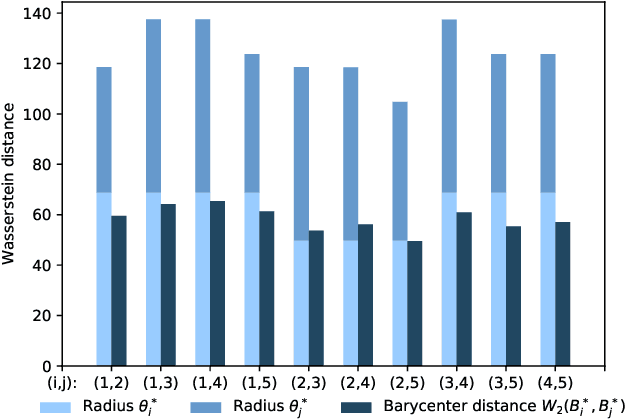
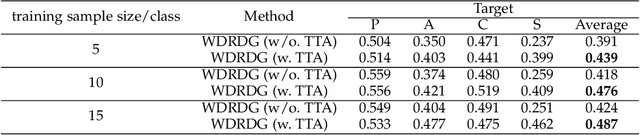
Domain generalization aims at learning a universal model that performs well on unseen target domains, incorporating knowledge from multiple source domains. In this research, we consider the scenario where different domain shifts occur among conditional distributions of different classes across domains. When labeled samples in the source domains are limited, existing approaches are not sufficiently robust. To address this problem, we propose a novel domain generalization framework called Wasserstein Distributionally Robust Domain Generalization (WDRDG), inspired by the concept of distributionally robust optimization. We encourage robustness over conditional distributions within class-specific Wasserstein uncertainty sets and optimize the worst-case performance of a classifier over these uncertainty sets. We further develop a test-time adaptation module leveraging optimal transport to quantify the relationship between the unseen target domain and source domains to make adaptive inference for target data. Experiments on the Rotated MNIST, PACS and the VLCS datasets demonstrate that our method could effectively balance the robustness and discriminability in challenging generalization scenarios.