Generalized Chernoff Sampling for Active Learning and Structured Bandit Algorithms
Paper and Code
Dec 15, 2020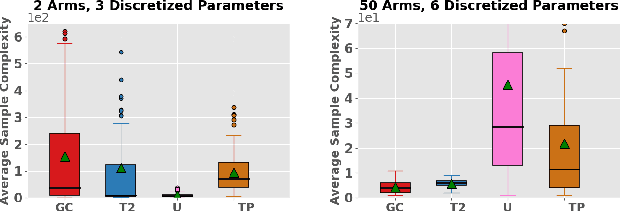
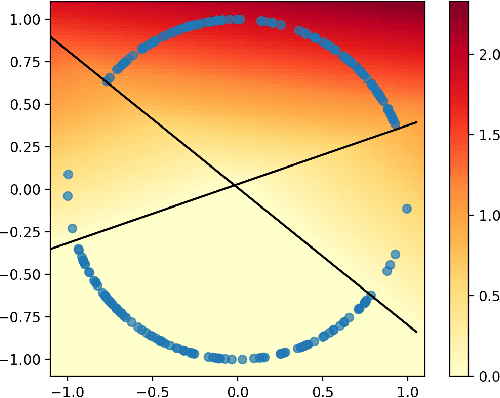
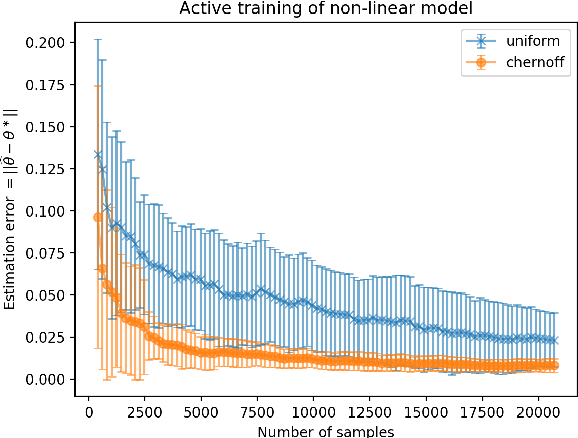
Active learning and structured stochastic bandit problems are intimately related to the classical problem of sequential experimental design. This paper studies active learning and best-arm identification in structured bandit settings from the viewpoint of active sequential hypothesis testing, a framework initiated by Chernoff (1959). We first characterize the sample complexity of Chernoff's original procedure by uncovering terms that reduce in significance as the allowed error probability $\delta \rightarrow 0$, but are nevertheless relevant at any fixed value of $\delta > 0$. While initially proposed for testing among finitely many hypotheses, we obtain the analogue of Chernoff sampling for the case when the hypotheses belong to a compact space. This makes it applicable to active learning and structured bandit problems, where the unknown parameter specifying the arm means is often assumed to be an element of Euclidean space. Empirically, we demonstrate the potential of our proposed approach for active learning of neural network models and in the linear bandit setting, where we observe that our general-purpose approach compares favorably to state-of-the-art methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge