Generalized Bandit Regret Minimizer Framework in Imperfect Information Extensive-Form Game
Paper and Code
Mar 28, 2022
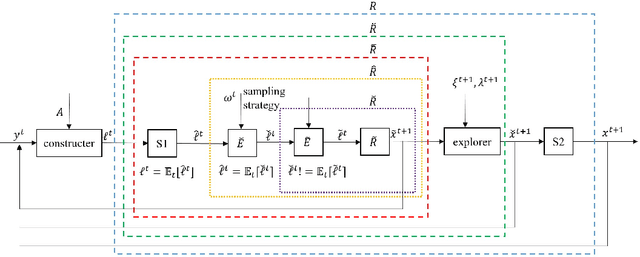
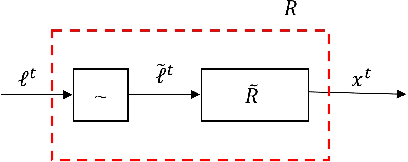
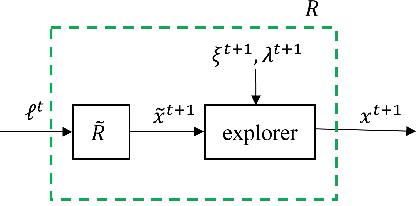
Regret minimization methods are a powerful tool for learning approximate Nash equilibrium (NE) in two-player zero-sum imperfect information extensive-form games (IIEGs). We consider the problem in the interactive bandit-feedback setting where we don't know the dynamics of the IIEG. In general, only the interactive trajectory and the reached terminal node value $v(z^t)$ are revealed. To learn NE, the regret minimizer is required to estimate the full-feedback loss gradient $\ell^t$ by $v(z^t)$ and minimize the regret. In this paper, we propose a generalized framework for this learning setting. It presents a theoretical framework for the design and the modular analysis of the bandit regret minimization methods. We demonstrate that the most recent bandit regret minimization methods can be analyzed as a particular case of our framework. Following this framework, we describe a novel method SIX-OMD to learn approximate NE. It is model-free and extremely improves the best existing convergence rate from the order of $O(\sqrt{X B/T}+\sqrt{Y C/T})$ to $O(\sqrt{ M_{\mathcal{X}}/T} +\sqrt{ M_{\mathcal{Y}}/T})$. Moreover, SIX-OMD is computationally efficient as it needs to perform the current strategy and average strategy updates only along the sampled trajectory.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge