Generalization Error Bounds for Iterative Recovery Algorithms Unfolded as Neural Networks
Paper and Code
Dec 08, 2021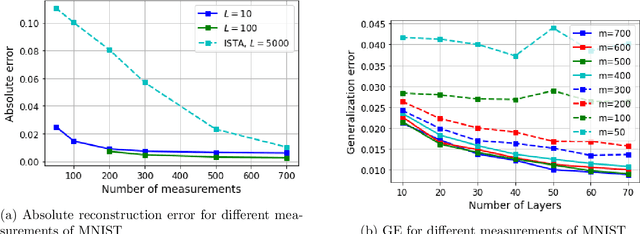
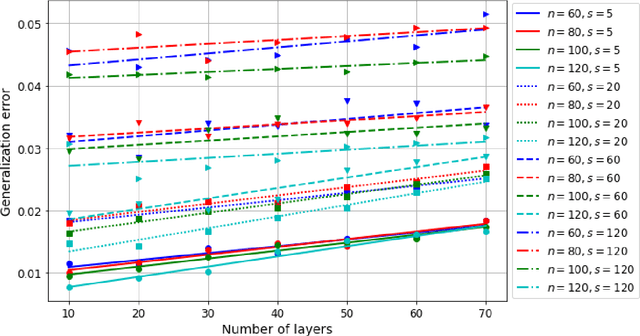
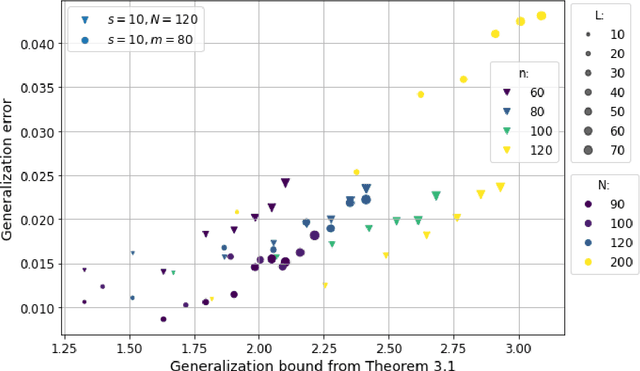
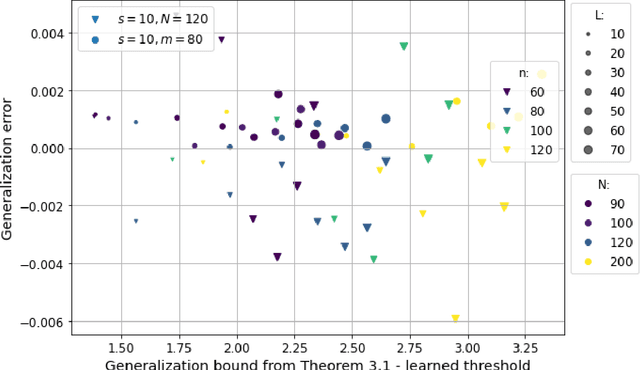
Motivated by the learned iterative soft thresholding algorithm (LISTA), we introduce a general class of neural networks suitable for sparse reconstruction from few linear measurements. By allowing a wide range of degrees of weight-sharing between the layers, we enable a unified analysis for very different neural network types, ranging from recurrent ones to networks more similar to standard feedforward neural networks. Based on training samples, via empirical risk minimization we aim at learning the optimal network parameters and thereby the optimal network that reconstructs signals from their low-dimensional linear measurements. We derive generalization bounds by analyzing the Rademacher complexity of hypothesis classes consisting of such deep networks, that also take into account the thresholding parameters. We obtain estimates of the sample complexity that essentially depend only linearly on the number of parameters and on the depth. We apply our main result to obtain specific generalization bounds for several practical examples, including different algorithms for (implicit) dictionary learning, and convolutional neural networks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge