Generalization Bounds via Conditional $f$-Information
Paper and Code
Oct 30, 2024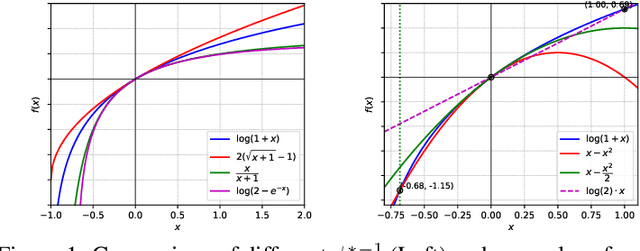
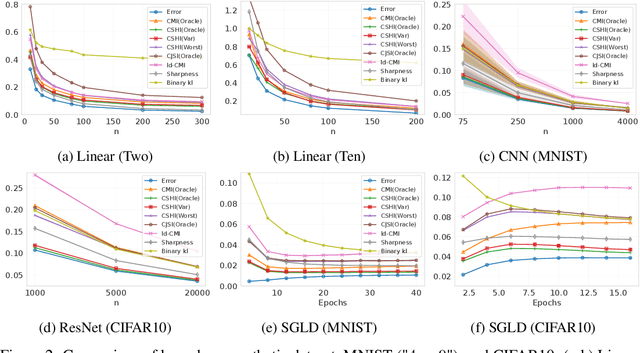
In this work, we introduce novel information-theoretic generalization bounds using the conditional $f$-information framework, an extension of the traditional conditional mutual information (MI) framework. We provide a generic approach to derive generalization bounds via $f$-information in the supersample setting, applicable to both bounded and unbounded loss functions. Unlike previous MI-based bounds, our proof strategy does not rely on upper bounding the cumulant-generating function (CGF) in the variational formula of MI. Instead, we set the CGF or its upper bound to zero by carefully selecting the measurable function invoked in the variational formula. Although some of our techniques are partially inspired by recent advances in the coin-betting framework (e.g., Jang et al. (2023)), our results are independent of any previous findings from regret guarantees of online gambling algorithms. Additionally, our newly derived MI-based bound recovers many previous results and improves our understanding of their potential limitations. Finally, we empirically compare various $f$-information measures for generalization, demonstrating the improvement of our new bounds over the previous bounds.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge