Fundamental Limits and Optimization of Multiband Sensing
Paper and Code
Jul 21, 2022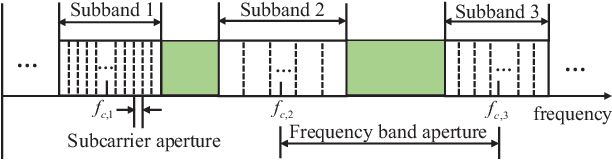
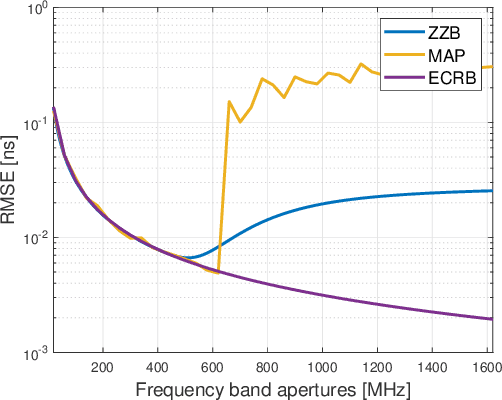
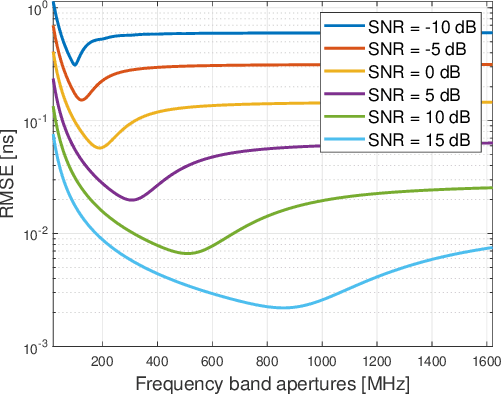
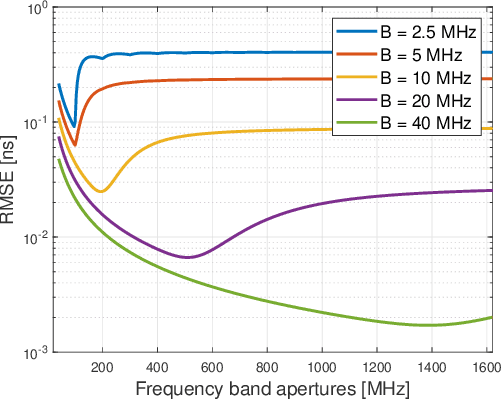
Multiband sensing is a promising technology that utilizes multiple non-contiguous frequency bands to achieve high-resolution target sensing. In this paper, we investigate the fundamental limits and optimization of multiband sensing, focusing on the fundamental limits associated with time delay. We first derive a Fisher information matrix (FIM) with a compact form using the Dirichlet kernel and then derive a closed-form expression of the Cramer-Rao bound (CRB) for the delay separation in a simplified case to reveal useful insights. Then, a metric called the statistical resolution limit (SRL) that provides a resolution limit is employed to investigate the fundamental limits of delay resolution. The fundamental limits of delay estimation are also investigated based on the CRB and Ziv-Zakai bound (ZZB). Based on the above derived fundamental limits, numerical results are presented to analyze the effect of frequency band apertures and phase distortions on the performance limits of the multiband sensing systems. We formulate an optimization problem to find the optimal system configuration in multiband sensing systems with the objective of minimizing the delay SRL. To solve this non-convex constrained problem, we propose an efficient alternating optimization (AO) algorithm which iteratively optimizes the variables using successive convex approximation (SCA) and one-dimensional search. Simulation results demonstrate the effectiveness of the proposed algorithm.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge