From the Greene--Wu Convolution to Gradient Estimation over Riemannian Manifolds

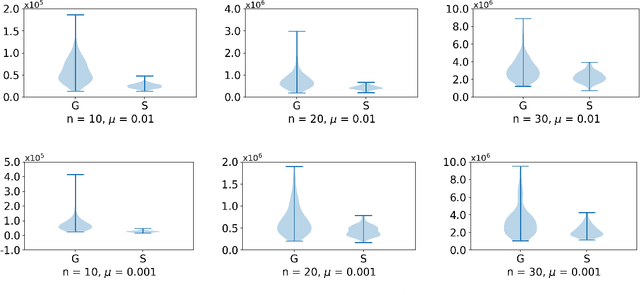
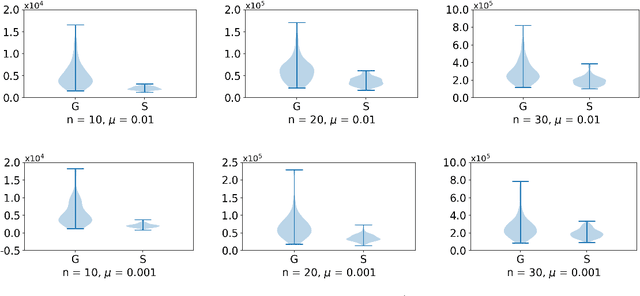
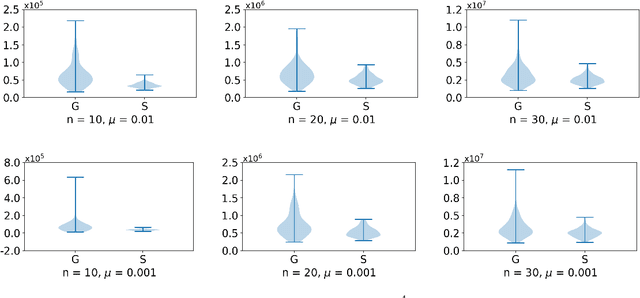
Over a complete Riemannian manifold of finite dimension, Greene and Wu introduced a convolution, known as Greene-Wu (GW) convolution. In this paper, we introduce a reformulation of the GW convolution. Using our reformulation, many properties of the GW convolution can be easily derived, including a new formula for how the curvature of the space would affect the curvature of the function through the GW convolution. Also enabled by our new reformulation, an improved method for gradient estimation over Riemannian manifolds is introduced. Theoretically, our gradient estimation method improves the order of estimation error from $O \left( \left( n + 3 \right)^{3/2} \right)$ to $O \left( n^{3/2} \right)$, where $n$ is the dimension of the manifold. Empirically, our method outperforms the best existing method for gradient estimation over Riemannian manifolds, as evidenced by thorough experimental evaluations.