Fourier Phase Retrieval with Extended Support Estimation via Deep Neural Network

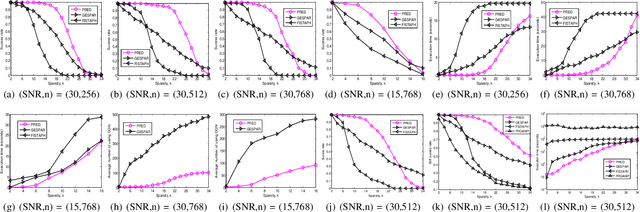
We consider the problem of sparse phase retrieval from Fourier transform magnitudes to recover $k$-sparse signal vector $x^{\circ}$ and its support $\mathcal{T}$. To improve the reconstruction performance of $x^{\circ}$, we exploit extended support estimate $\mathcal{E}$ of size larger than $k$ satisfying $\mathcal{E} \supseteq \mathcal{T}$. We propose a learning method for the deep neural network to provide $\mathcal{E}$ as an union of equivalent solutions of $\mathcal{T}$ by utilizing modulo Fourier invariances and suggest a searching technique for $\mathcal{T}$ by iteratively sampling $\mathcal{E}$ from the trained network output and applying the hard thresholding to $\mathcal{E}$. Numerical results show that our proposed scheme has a superior performance with a lower complexity compared to the local search-based greedy sparse phase retrieval method and a state-of-the-art variant of the Fienup method.