For Manifold Learning, Deep Neural Networks can be Locality Sensitive Hash Functions
Paper and Code
Mar 11, 2021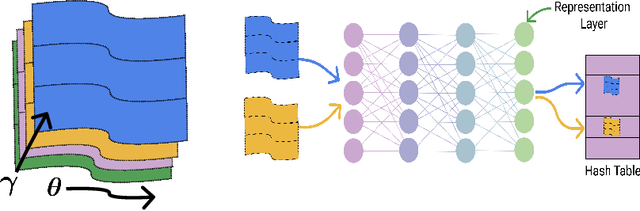
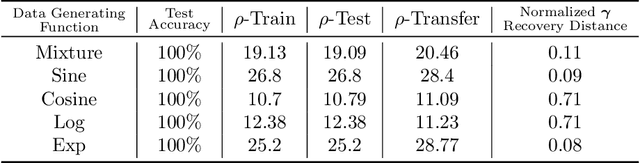

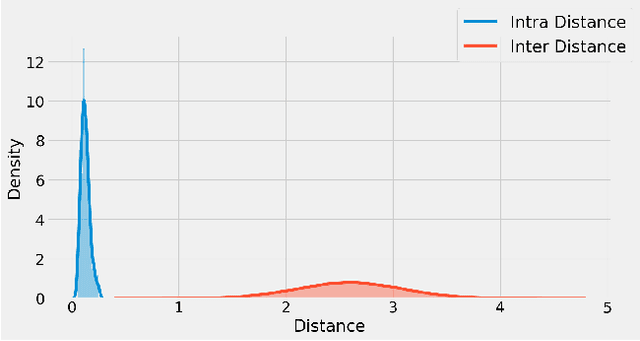
It is well established that training deep neural networks gives useful representations that capture essential features of the inputs. However, these representations are poorly understood in theory and practice. In the context of supervised learning an important question is whether these representations capture features informative for classification, while filtering out non-informative noisy ones. We explore a formalization of this question by considering a generative process where each class is associated with a high-dimensional manifold and different classes define different manifolds. Under this model, each input is produced using two latent vectors: (i) a "manifold identifier" $\gamma$ and; (ii)~a "transformation parameter" $\theta$ that shifts examples along the surface of a manifold. E.g., $\gamma$ might represent a canonical image of a dog, and $\theta$ might stand for variations in pose, background or lighting. We provide theoretical and empirical evidence that neural representations can be viewed as LSH-like functions that map each input to an embedding that is a function of solely the informative $\gamma$ and invariant to $\theta$, effectively recovering the manifold identifier $\gamma$. An important consequence of this behavior is one-shot learning to unseen classes.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge