Fluorescent wavefront shaping using incoherent iterative phase conjugation
Paper and Code
May 15, 2022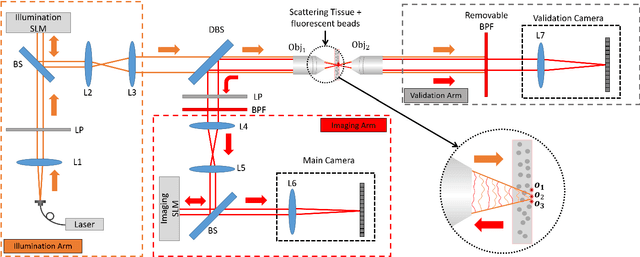
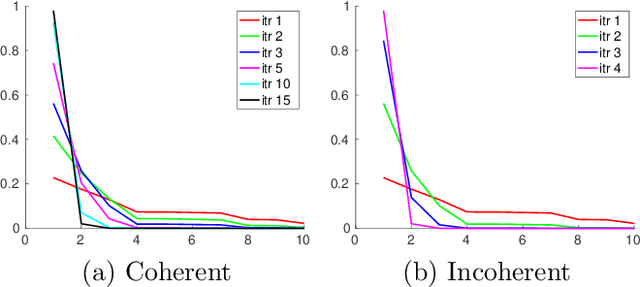

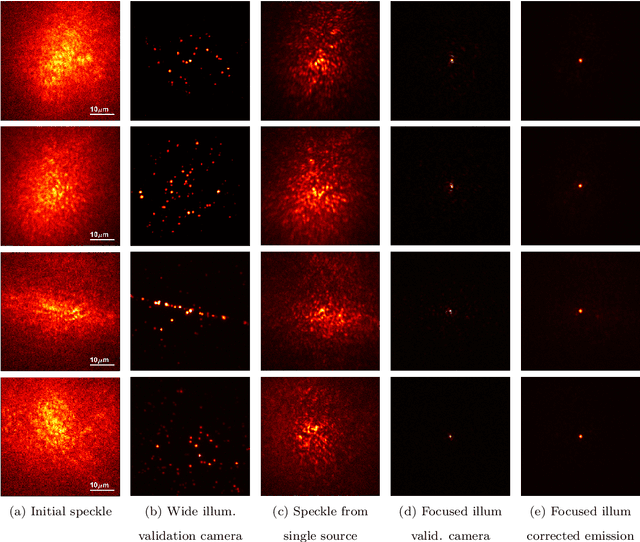
Wavefront shaping correction makes it possible to image fluorescent particles deep inside scattering tissue. This requires determining a correction mask to be placed in both excitation and emission paths. Standard approaches select correction masks by optimizing various image metrics, a process that requires capturing a prohibitively large number of images. To reduce acquisition cost, iterative phase conjugation techniques use the observation that the desired correction mask is an eigenvector of the tissue transmission operator. They then determine this eigenvector via optical implementations of the power iteration method, which require capturing orders of magnitude fewer images. Existing iterative phase conjugation techniques assume a linear model for the transmission of light through tissue, and thus only apply to fully-coherent imaging systems. We extend such techniques to the incoherent case for the first time. The fact that light emitted from different sources sums incoherently violates the linear model and makes linear transmission operators inapplicable. We show that, surprisingly, the non-linearity due to incoherent summation results in an order-of-magnitude acceleration in the convergence of the phase conjugation iteration.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge