Flow Field Reconstructions with GANs based on Radial Basis Functions
Paper and Code
Aug 11, 2020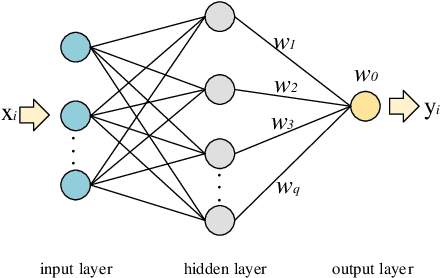
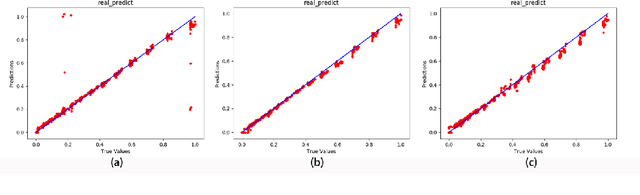
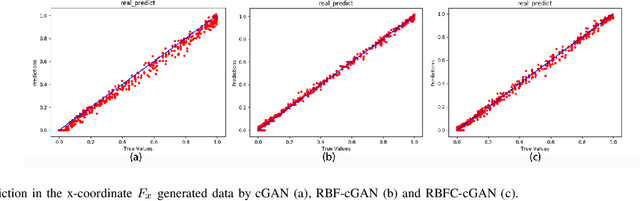
Nonlinear sparse data regression and generation have been a long-term challenge, to cite the flow field reconstruction as a typical example. The huge computational cost of computational fluid dynamics (CFD) makes it much expensive for large scale CFD data producing, which is the reason why we need some cheaper ways to do this, of which the traditional reduced order models (ROMs) were promising but they couldn't generate a large number of full domain flow field data (FFD) to realize high-precision flow field reconstructions. Motivated by the problems of existing approaches and inspired by the success of the generative adversarial networks (GANs) in the field of computer vision, we prove an optimal discriminator theorem that the optimal discriminator of a GAN is a radial basis function neural network (RBFNN) while dealing with nonlinear sparse FFD regression and generation. Based on this theorem, two radial basis function-based GANs (RBF-GAN and RBFC-GAN), for regression and generation purposes, are proposed. Three different datasets are applied to verify the feasibility of our models. The results show that the performance of the RBF-GAN and the RBFC-GAN are better than that of GANs/cGANs by means of both the mean square error (MSE) and the mean square percentage error (MSPE). Besides, compared with GANs/cGANs, the stability of the RBF-GAN and the RBFC-GAN improve by 34.62% and 72.31%, respectively. Consequently, our proposed models can be used to generate full domain FFD from limited and sparse datasets, to meet the requirement of high-precision flow field reconstructions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge