Fitting Spectral Decay with the $k$-Support Norm
Paper and Code
Jan 04, 2016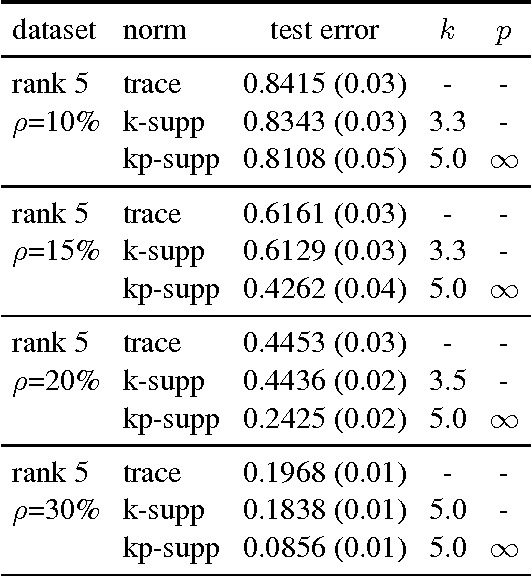
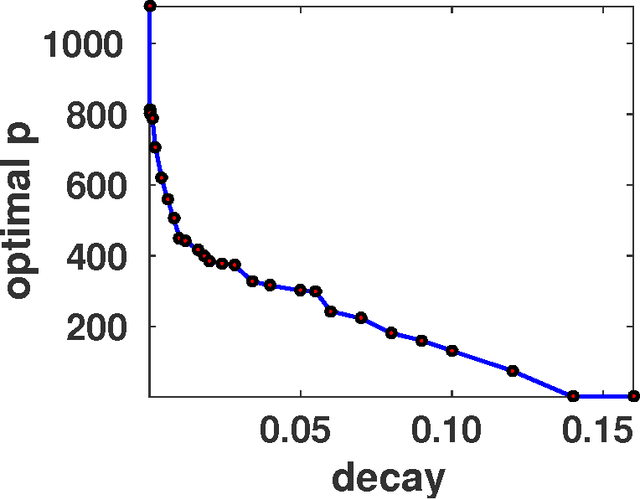
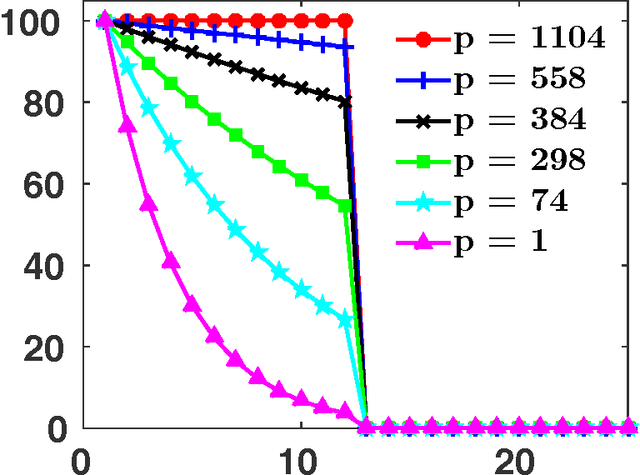

The spectral $k$-support norm enjoys good estimation properties in low rank matrix learning problems, empirically outperforming the trace norm. Its unit ball is the convex hull of rank $k$ matrices with unit Frobenius norm. In this paper we generalize the norm to the spectral $(k,p)$-support norm, whose additional parameter $p$ can be used to tailor the norm to the decay of the spectrum of the underlying model. We characterize the unit ball and we explicitly compute the norm. We further provide a conditional gradient method to solve regularization problems with the norm, and we derive an efficient algorithm to compute the Euclidean projection on the unit ball in the case $p=\infty$. In numerical experiments, we show that allowing $p$ to vary significantly improves performance over the spectral $k$-support norm on various matrix completion benchmarks, and better captures the spectral decay of the underlying model.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge