First-Order Problem Solving through Neural MCTS based Reinforcement Learning
Paper and Code
Jan 11, 2021
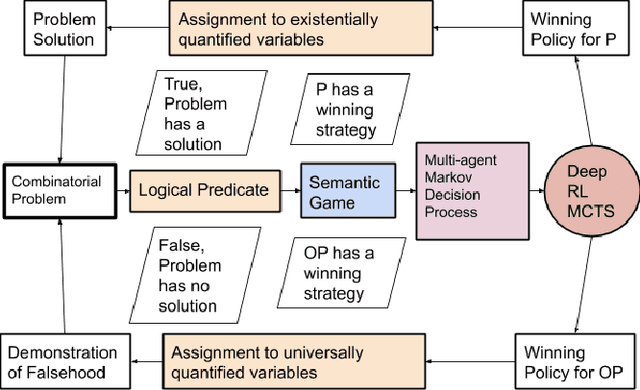
The formal semantics of an interpreted first-order logic (FOL) statement can be given in Tarskian Semantics or a basically equivalent Game Semantics. The latter maps the statement and the interpretation into a two-player semantic game. Many combinatorial problems can be described using interpreted FOL statements and can be mapped into a semantic game. Therefore, learning to play a semantic game perfectly leads to the solution of a specific instance of a combinatorial problem. We adapt the AlphaZero algorithm so that it becomes better at learning to play semantic games that have different characteristics than Go and Chess. We propose a general framework, Persephone, to map the FOL description of a combinatorial problem to a semantic game so that it can be solved through a neural MCTS based reinforcement learning algorithm. Our goal for Persephone is to make it tabula-rasa, mapping a problem stated in interpreted FOL to a solution without human intervention.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge