Finite mixture models are typically inconsistent for the number of components

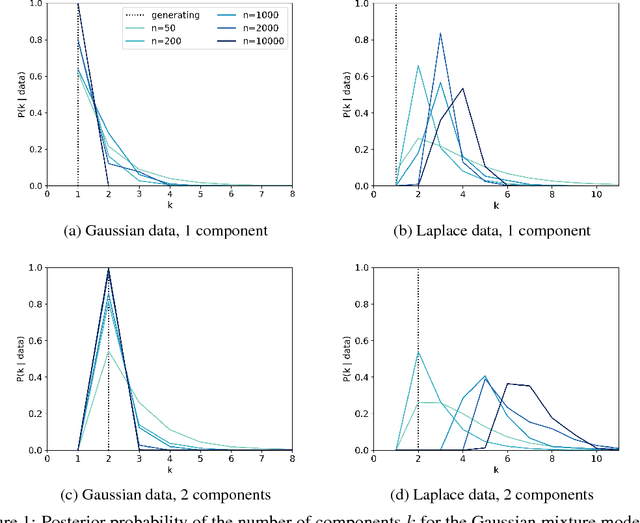
Scientists and engineers are often interested in learning the number of subpopulations (or components) present in a data set. Practitioners commonly use a Dirichlet process mixture model (DPMM) for this purpose; in particular, they count the number of clusters---i.e. components containing at least one data point---in the DPMM posterior. But Miller and Harrison (2013) warn that the DPMM cluster-count posterior is severely inconsistent for the number of latent components when the data are truly generated from a finite mixture; that is, the cluster-count posterior probability on the true generating number of components goes to zero in the limit of infinite data. A potential alternative is to use a finite mixture model (FMM) with a prior on the number of components. Past work has shown the resulting FMM component-count posterior is consistent. But existing results crucially depend on the assumption that the component likelihoods are perfectly specified. In practice, this assumption is unrealistic, and empirical evidence (Miller and Dunson, 2019) suggests that the FMM posterior on the number of components is sensitive to the likelihood choice. In this paper, we add rigor to data-analysis folk wisdom by proving that under even the slightest model misspecification, the FMM posterior on the number of components is ultraseverely inconsistent: for any finite $k \in \mathbb{N}$, the posterior probability that the number of components is $k$ converges to 0 in the limit of infinite data. We illustrate practical consequences of our theory on simulated and real data sets.