Federated Stochastic Primal-dual Learning with Differential Privacy
Paper and Code
Apr 26, 2022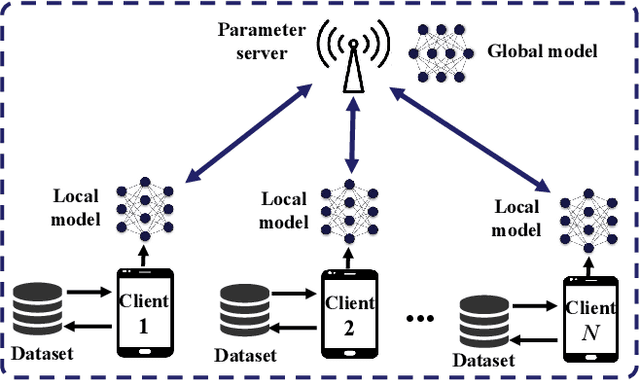
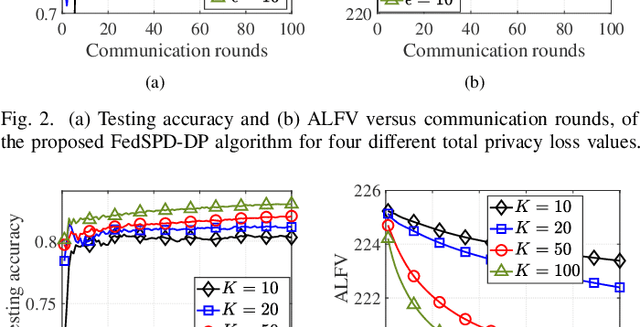
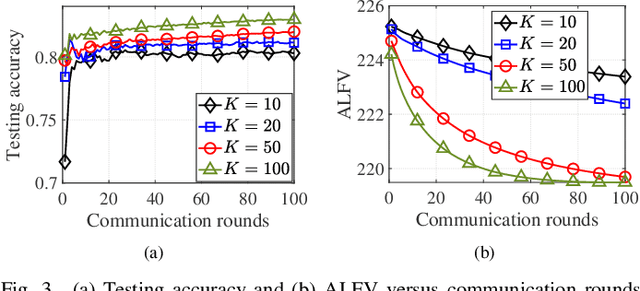
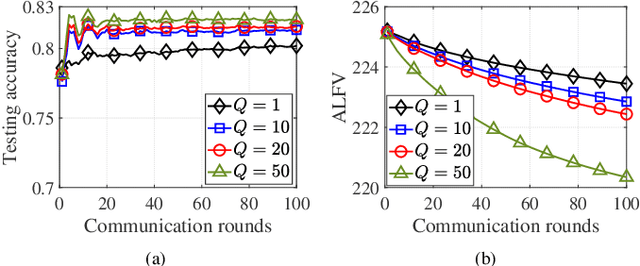
Federated learning (FL) is a new paradigm that enables many clients to jointly train a machine learning (ML) model under the orchestration of a parameter server while keeping the local data not being exposed to any third party. However, the training of FL is an interactive process between local clients and the parameter server. Such process would cause privacy leakage since adversaries may retrieve sensitive information by analyzing the overheard messages. In this paper, we propose a new federated stochastic primal-dual algorithm with differential privacy (FedSPD-DP). Compared to the existing methods, the proposed FedSPD-DP incorporates local stochastic gradient descent (local SGD) and partial client participation (PCP) for addressing the issues of communication efficiency and straggler effects due to randomly accessed clients. Our analysis shows that the data sampling strategy and PCP can enhance the data privacy whereas the larger number of local SGD steps could increase privacy leakage, revealing a non-trivial tradeoff between algorithm communication efficiency and privacy protection. Specifically, we show that, by guaranteeing $(\epsilon, \delta)$-DP for each client per communication round, the proposed algorithm guarantees $(\mathcal{O}(q\epsilon \sqrt{p T}), \delta)$-DP after $T$ communication rounds while maintaining an $\mathcal{O}(1/\sqrt{pTQ})$ convergence rate for a convex and non-smooth learning problem, where $Q$ is the number of local SGD steps, $p$ is the client sampling probability, $q=\max_{i} q_i/\sqrt{1-q_i}$ and $q_i$ is the data sampling probability of each client under PCP. Experiment results are presented to evaluate the practical performance of the proposed algorithm and comparison with state-of-the-art methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge