Federated Learning with Lossy Distributed Source Coding: Analysis and Optimization

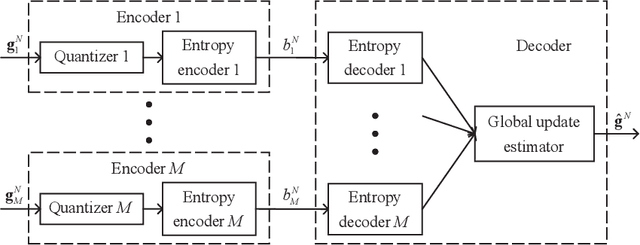
Recently, federated learning (FL), which replaces data sharing with model sharing, has emerged as an efficient and privacy-friendly paradigm for machine learning (ML). A main challenge of FL is its huge uplink communication cost. In this paper, we tackle this challenge from an information-theoretic perspective. Specifically, we put forth a distributed source coding (DSC) framework for FL uplink, which unifies the encoding, transmission, and aggregation of the local updates as a lossy DSC problem, thus providing a systematic way to exploit the correlation between local updates to improve the uplink efficiency. Under this DSC-FL framework, we propose an FL uplink scheme based on the modified Berger-Tung coding (MBTC), which supports separate encoding and joint decoding by modifying the achievability scheme of the Berger-Tung inner bound. The achievable region of the MBTC-based uplink scheme is also derived. To unleash the potential of the MBTC-based FL scheme, we carry out a convergence analysis and then formulate a convergence rate maximization problem to optimize the parameters of MBTC. To solve this problem, we develop two algorithms, respectively for small- and large-scale FL systems, based on the majorization-minimization (MM) technique. Numerical results demonstrate the superiority of the MBTC-based FL scheme in terms of aggregation distortion, convergence performance, and communication cost, revealing the great potential of the DSC-FL framework.