Feature Selection via the Intervened Interpolative Decomposition and its Application in Diversifying Quantitative Strategies
Paper and Code
Sep 29, 2022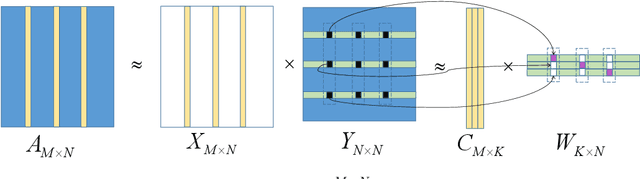
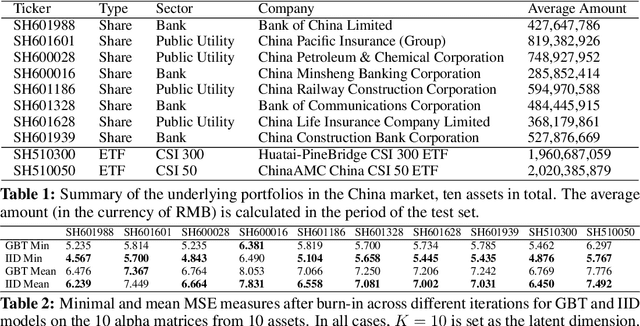
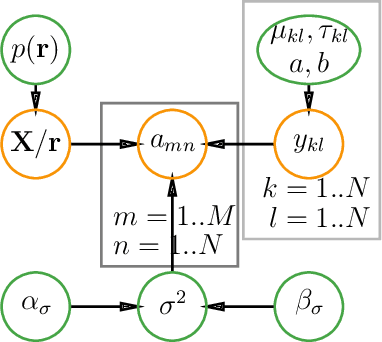

In this paper, we propose a probabilistic model for computing an interpolative decomposition (ID) in which each column of the observed matrix has its own priority or importance, so that the end result of the decomposition finds a set of features that are representative of the entire set of features, and the selected features also have higher priority than others. This approach is commonly used for low-rank approximation, feature selection, and extracting hidden patterns in data, where the matrix factors are latent variables associated with each data dimension. Gibbs sampling for Bayesian inference is applied to carry out the optimization. We evaluate the proposed models on real-world datasets, including ten Chinese A-share stocks, and demonstrate that the proposed Bayesian ID algorithm with intervention (IID) produces comparable reconstructive errors to existing Bayesian ID algorithms while selecting features with higher scores or priority.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge