Fatigued Random Walks in Hypergraphs: A Neuronal Analogy to Improve Retrieval Performance
Paper and Code
Apr 12, 2021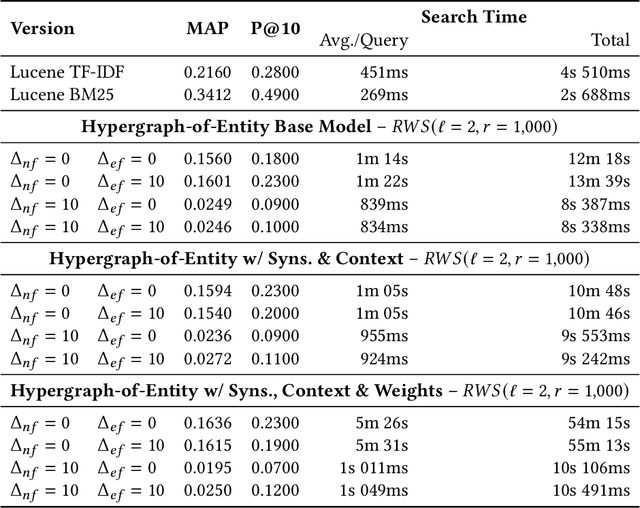
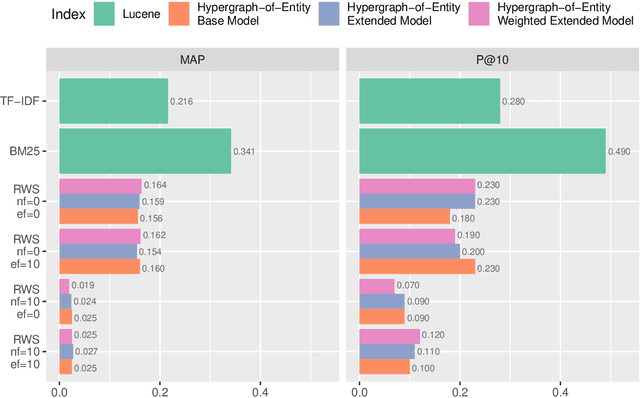
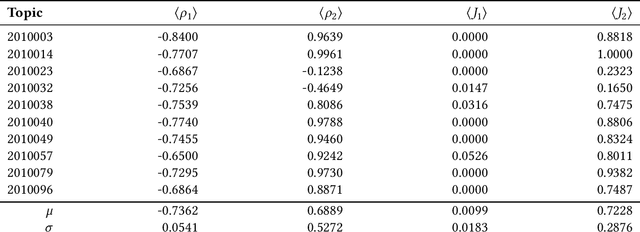
Hypergraphs are data structures capable of capturing supra-dyadic relations. We can use them to model binary relations, but also to model groups of entities, as well as the intersections between these groups or the contained subgroups. In previous work, we explored the usage of hypergraphs as an indexing data structure, in particular one that was capable of seamlessly integrating text, entities and their relations to support entity-oriented search tasks. As more information is added to the hypergraph, however, it not only increases in size, but it also becomes denser, making the task of efficiently ranking nodes or hyperedges more complex. Random walks can effectively capture network structure, without compromising performance, or at least providing a tunable balance between efficiency and effectiveness, within a nondeterministic universe. For a higher effectiveness, a higher number of random walks is usually required, which often results in lower efficiency. Inspired by von Neumann and the neuron in the brain, we propose and study the usage of node and hyperedge fatigue as a way to temporarily constrict random walks during keyword-based ad hoc retrieval. We found that we were able to improve search time by a factor of 32, but also worsen MAP by a factor of 8. Moreover, by distinguishing between fatigue in nodes and hyperedges, we are able to find that, for hyperedge ranking tasks, we consistently obtained lower MAP scores when increasing fatigue for nodes. On the other hand, the overall impact of hyperedge fatigue was slightly positive, although it also slightly worsened efficiency.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge