Faster Rates for Compressed Federated Learning with Client-Variance Reduction

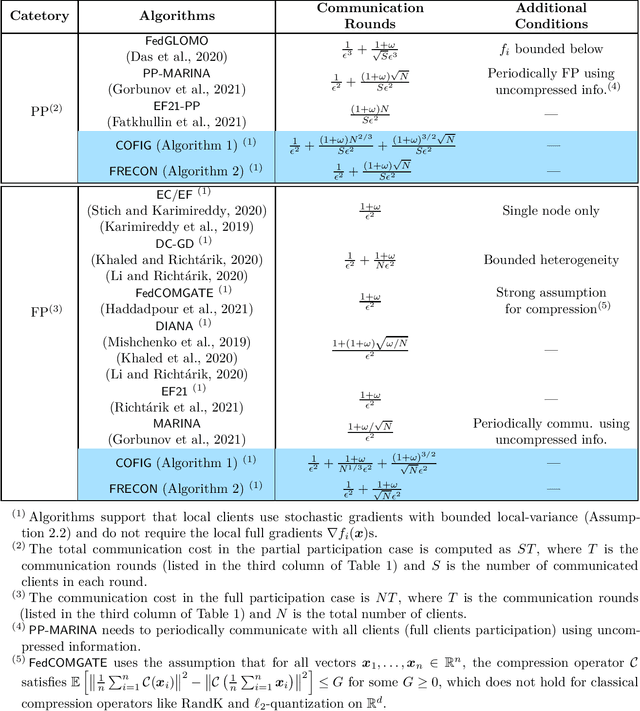
Due to the communication bottleneck in distributed and federated learning applications, algorithms using communication compression have attracted significant attention and are widely used in practice. Moreover, there exists client-variance in federated learning due to the total number of heterogeneous clients is usually very large and the server is unable to communicate with all clients in each communication round. In this paper, we address these two issues together by proposing compressed and client-variance reduced methods. Concretely, we introduce COFIG and FRECON, which successfully enjoy communication compression with client-variance reduction. The total communication round of COFIG is $O(\frac{(1+\omega)^{3/2}\sqrt{N}}{S\epsilon^2}+\frac{(1+\omega)N^{2/3}}{S\epsilon^2})$ in the nonconvex setting, where $N$ is the total number of clients, $S$ is the number of communicated clients in each round, $\epsilon$ is the convergence error, and $\omega$ is the parameter for the compression operator. Besides, our FRECON can converge faster than COFIG in the nonconvex setting, and it converges with $O(\frac{(1+\omega)\sqrt{N}}{S\epsilon^2})$ communication rounds. In the convex setting, COFIG converges within the communication rounds $O(\frac{(1+\omega)\sqrt{N}}{S\epsilon})$, which is also the first convergence result for compression schemes that do not communicate with all the clients in each round. In sum, both COFIG and FRECON do not need to communicate with all the clients and provide first/faster convergence results for convex and nonconvex federated learning, while previous works either require full clients communication (thus not practical) or obtain worse convergence results.