Faster PET Reconstruction with Non-Smooth Priors by Randomization and Preconditioning

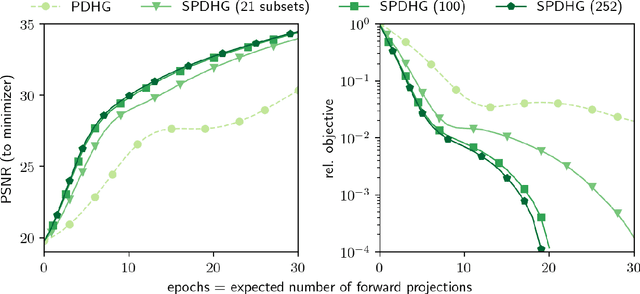
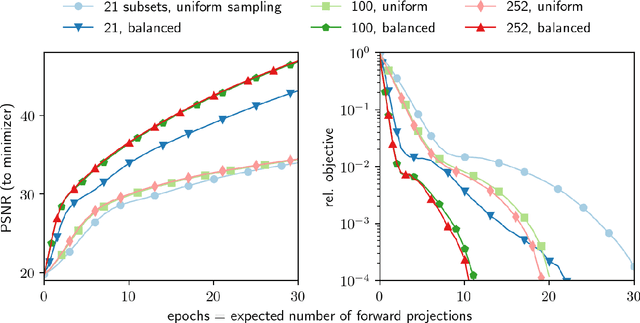
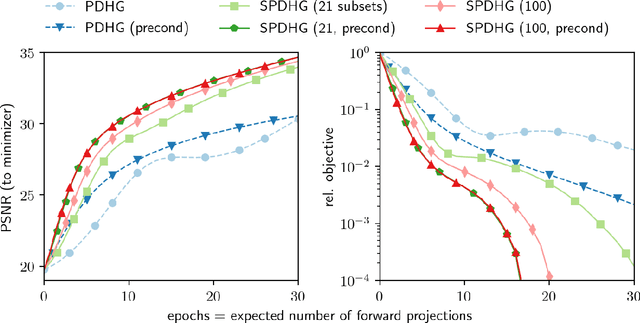
Uncompressed clinical data from modern positron emission tomography (PET) scanners are very large, exceeding 350 million data points. The last decades have seen tremendous advancements in mathematical imaging tools many of which lead to non-smooth optimization problems. Most of these tools have not been translated to clinical PET data, as the algorithms for non-smooth problems do not scale well enough for large data sets. In this work, inspired by big data machine learning applications, we use advanced randomized optimization algorithms to solve the PET reconstruction problem for a very large class of non-smooth priors which includes for example total variation, total generalized variation, directional total variation and many constraints. We show on real PET data (FDG and florbetapir) from a Siemens Biograph mMR that a dozen forward (and back) projections are sufficient for a variety of mathematical models to produce clinically relevant images; thus showing that the proposed algorithm is fast enough to bring these models into routine clinical practice. Moreover, the proposed algorithm is as fast on the unregularized problem as the clinical standard OSEM but-in contrast to OSEM-has provable convergence guarantees, robustness and stability for any subset selection.