Faster Kernel Matrix Algebra via Density Estimation
Paper and Code
Feb 16, 2021
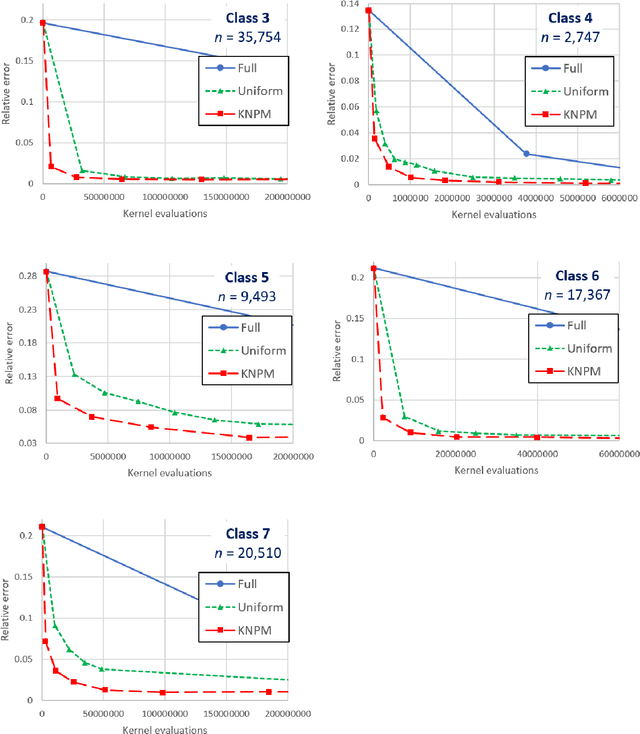
We study fast algorithms for computing fundamental properties of a positive semidefinite kernel matrix $K \in \mathbb{R}^{n \times n}$ corresponding to $n$ points $x_1,\ldots,x_n \in \mathbb{R}^d$. In particular, we consider estimating the sum of kernel matrix entries, along with its top eigenvalue and eigenvector. We show that the sum of matrix entries can be estimated to $1+\epsilon$ relative error in time $sublinear$ in $n$ and linear in $d$ for many popular kernels, including the Gaussian, exponential, and rational quadratic kernels. For these kernels, we also show that the top eigenvalue (and an approximate eigenvector) can be approximated to $1+\epsilon$ relative error in time $subquadratic$ in $n$ and linear in $d$. Our algorithms represent significant advances in the best known runtimes for these problems. They leverage the positive definiteness of the kernel matrix, along with a recent line of work on efficient kernel density estimation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge