Faster K-Means Cluster Estimation
Paper and Code
Jan 17, 2017

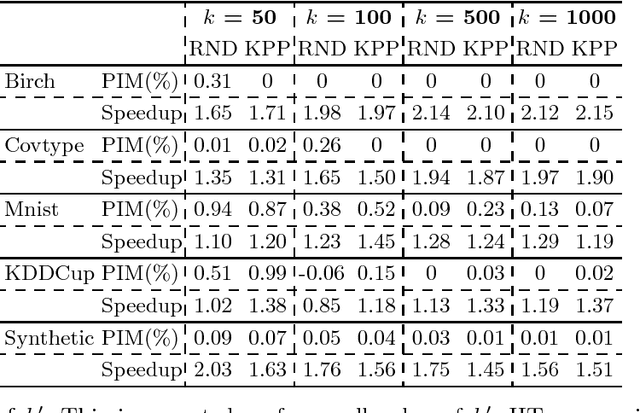
There has been considerable work on improving popular clustering algorithm `K-means' in terms of mean squared error (MSE) and speed, both. However, most of the k-means variants tend to compute distance of each data point to each cluster centroid for every iteration. We propose a fast heuristic to overcome this bottleneck with only marginal increase in MSE. We observe that across all iterations of K-means, a data point changes its membership only among a small subset of clusters. Our heuristic predicts such clusters for each data point by looking at nearby clusters after the first iteration of k-means. We augment well known variants of k-means with our heuristic to demonstrate effectiveness of our heuristic. For various synthetic and real-world datasets, our heuristic achieves speed-up of up-to 3 times when compared to efficient variants of k-means.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge