Faster algorithms for learning to link, align sequences, and price two-part tariffs
Paper and Code
Apr 07, 2022

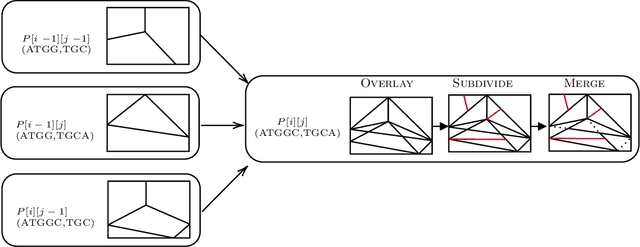

Data-driven algorithm configuration is a promising, learning-based approach for beyond worst-case analysis of algorithms with tunable parameters. An important open problem is the design of efficient data-driven algorithms for algorithm families with more than one parameter. In this work we provide algorithms for efficient (output-polynomial) multidimensional parameter tuning, i.e. for families with a small constant number of parameters, for three very different combinatorial problems -- linkage-based clustering, dynamic programming for sequence alignment, and auction design for two-part tariff schemes. We extend the single-parameter clustering algorithm of Balcan et al. 2020 arXiv:1907.00533 to multiple parameters and to the sequence alignment problem by proposing an execution graph which compactly represents all the states the algorithm could attain for all possible parameter values. A key problem-specific challenge is to efficiently compute how the partition of the parameter space (into regions with unique algorithmic states) changes with a single algorithmic step. We give algorithms which improve on the runtime of previously best known results for linkage-based clustering, sequence alignment and two-part tariff pricing.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge