Fast spatial inference in the homogeneous Ising model

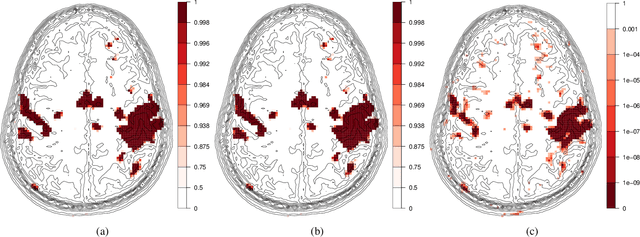
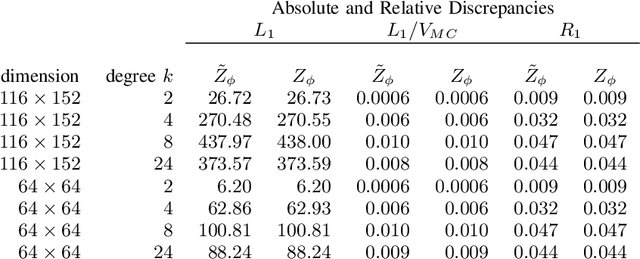
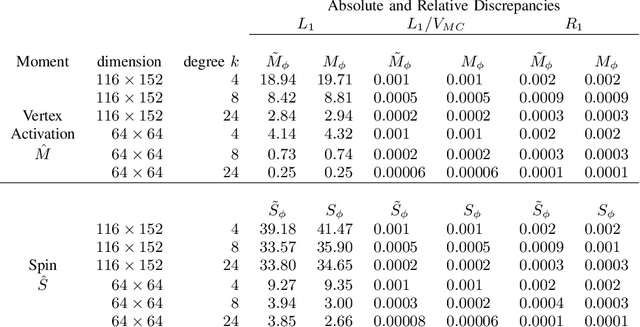
The Ising model is important in statistical modeling and inference in many applications, however its normalizing constant, mean number of active vertices and mean spin interaction are intractable. We provide accurate approximations that make it possible to calculate these quantities numerically. Simulation studies indicate good performance when compared to Markov Chain Monte Carlo methods and at a tiny fraction of the time. The methodology is also used to perform Bayesian inference in a functional Magnetic Resonance Imaging activation detection experiment.