Fast Prediction with SVM Models Containing RBF Kernels
Paper and Code
Oct 03, 2014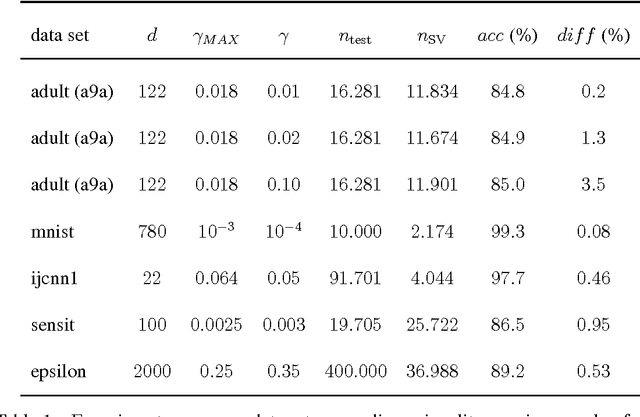

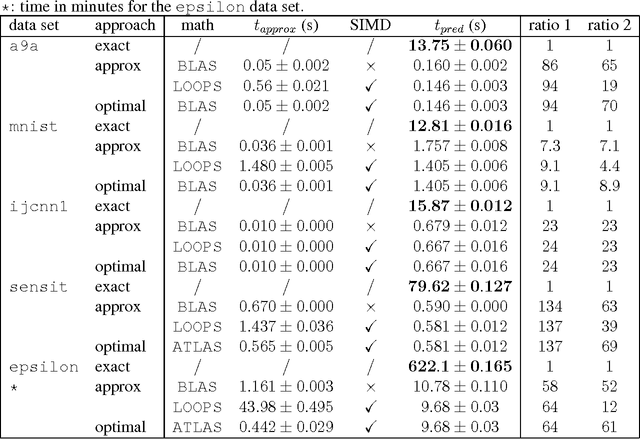
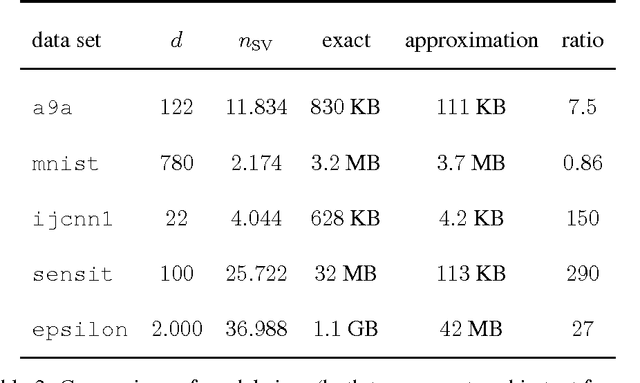
We present an approximation scheme for support vector machine models that use an RBF kernel. A second-order Maclaurin series approximation is used for exponentials of inner products between support vectors and test instances. The approximation is applicable to all kernel methods featuring sums of kernel evaluations and makes no assumptions regarding data normalization. The prediction speed of approximated models no longer relates to the amount of support vectors but is quadratic in terms of the number of input dimensions. If the number of input dimensions is small compared to the amount of support vectors, the approximated model is significantly faster in prediction and has a smaller memory footprint. An optimized C++ implementation was made to assess the gain in prediction speed in a set of practical tests. We additionally provide a method to verify the approximation accuracy, prior to training models or during run-time, to ensure the loss in accuracy remains acceptable and within known bounds.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge