Fast post-process Bayesian inference with Sparse Variational Bayesian Monte Carlo
Paper and Code
Mar 09, 2023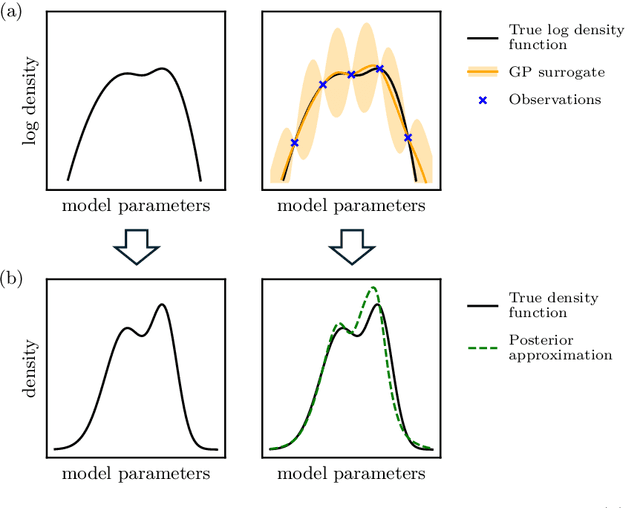
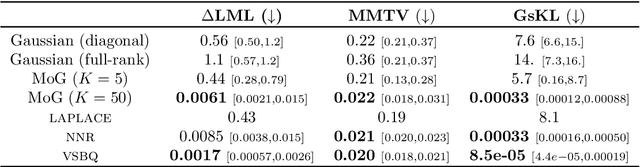
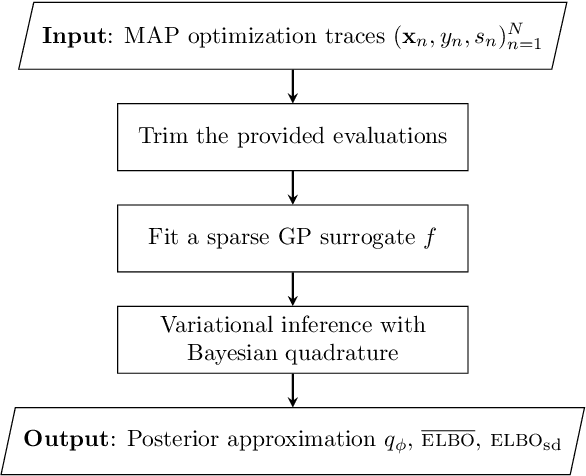
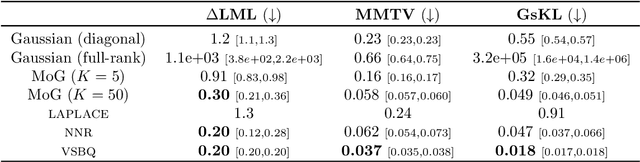
We introduce Sparse Variational Bayesian Monte Carlo (SVBMC), a method for fast "post-process" Bayesian inference for models with black-box and potentially noisy likelihoods. SVBMC reuses all existing target density evaluations -- for example, from previous optimizations or partial Markov Chain Monte Carlo runs -- to build a sparse Gaussian process (GP) surrogate model of the log posterior density. Uncertain regions of the surrogate are then refined via active learning as needed. Our work builds on the Variational Bayesian Monte Carlo (VBMC) framework for sample-efficient inference, with several novel contributions. First, we make VBMC scalable to a large number of pre-existing evaluations via sparse GP regression, deriving novel Bayesian quadrature formulae and acquisition functions for active learning with sparse GPs. Second, we introduce noise shaping, a general technique to induce the sparse GP approximation to focus on high posterior density regions. Third, we prove theoretical results in support of the SVBMC refinement procedure. We validate our method on a variety of challenging synthetic scenarios and real-world applications. We find that SVBMC consistently builds good posterior approximations by post-processing of existing model evaluations from different sources, often requiring only a small number of additional density evaluations.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge