Fast Point Cloud Geometry Compression with Context-based Residual Coding and INR-based Refinement
Paper and Code
Aug 06, 2024
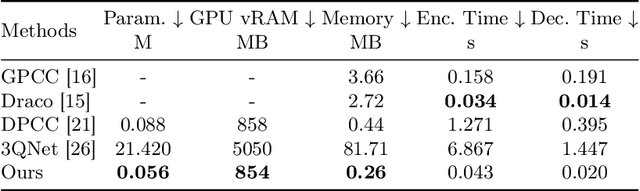


Compressing a set of unordered points is far more challenging than compressing images/videos of regular sample grids, because of the difficulties in characterizing neighboring relations in an irregular layout of points. Many researchers resort to voxelization to introduce regularity, but this approach suffers from quantization loss. In this research, we use the KNN method to determine the neighborhoods of raw surface points. This gives us a means to determine the spatial context in which the latent features of 3D points are compressed by arithmetic coding. As such, the conditional probability model is adaptive to local geometry, leading to significant rate reduction. Additionally, we propose a dual-layer architecture where a non-learning base layer reconstructs the main structures of the point cloud at low complexity, while a learned refinement layer focuses on preserving fine details. This design leads to reductions in model complexity and coding latency by two orders of magnitude compared to SOTA methods. Moreover, we incorporate an implicit neural representation (INR) into the refinement layer, allowing the decoder to sample points on the underlying surface at arbitrary densities. This work is the first to effectively exploit content-aware local contexts for compressing irregular raw point clouds, achieving high rate-distortion performance, low complexity, and the ability to function as an arbitrary-scale upsampling network simultaneously.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge