Fast PDE-constrained optimization via self-supervised operator learning
Paper and Code
Oct 25, 2021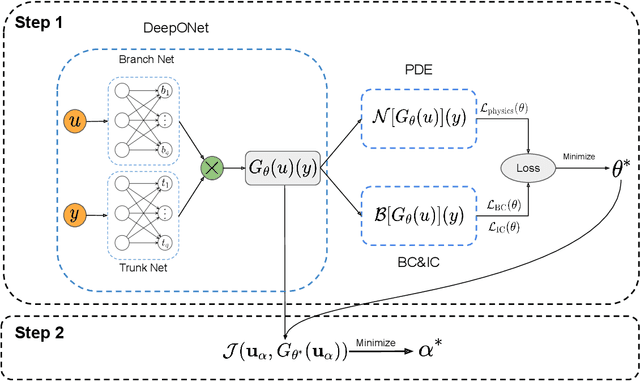

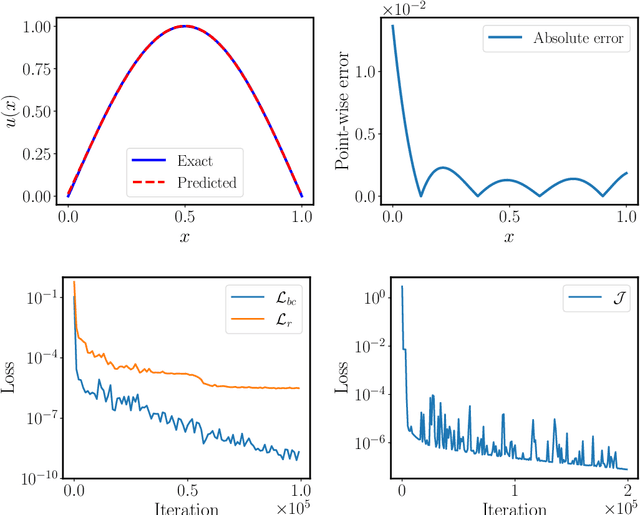
Design and optimal control problems are among the fundamental, ubiquitous tasks we face in science and engineering. In both cases, we aim to represent and optimize an unknown (black-box) function that associates a performance/outcome to a set of controllable variables through an experiment. In cases where the experimental dynamics can be described by partial differential equations (PDEs), such problems can be mathematically translated into PDE-constrained optimization tasks, which quickly become intractable as the number of control variables and the cost of experiments increases. In this work we leverage physics-informed deep operator networks (DeepONets) -- a self-supervised framework for learning the solution operator of parametric PDEs -- to build fast and differentiable surrogates for rapidly solving PDE-constrained optimization problems, even in the absence of any paired input-output training data. The effectiveness of the proposed framework will be demonstrated across different applications involving continuous functions as control or design variables, including time-dependent optimal control of heat transfer, and drag minimization of obstacles in Stokes flow. In all cases, we observe that DeepONets can minimize high-dimensional cost functionals in a matter of seconds, yielding a significant speed up compared to traditional adjoint PDE solvers that are typically costly and limited to relatively low-dimensional control/design parametrizations.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge