Fast Meta-Learning for Adaptive Hierarchical Classifier Design
Paper and Code
Nov 09, 2017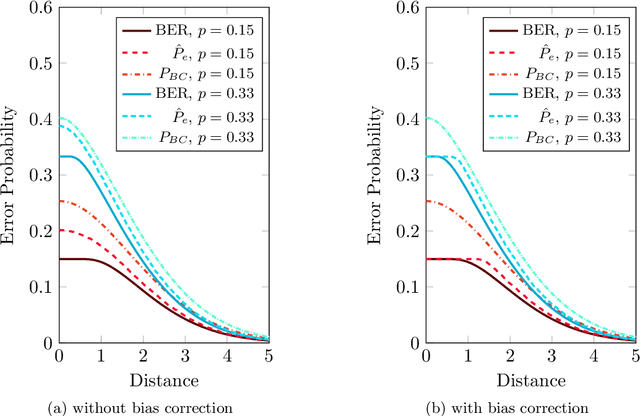
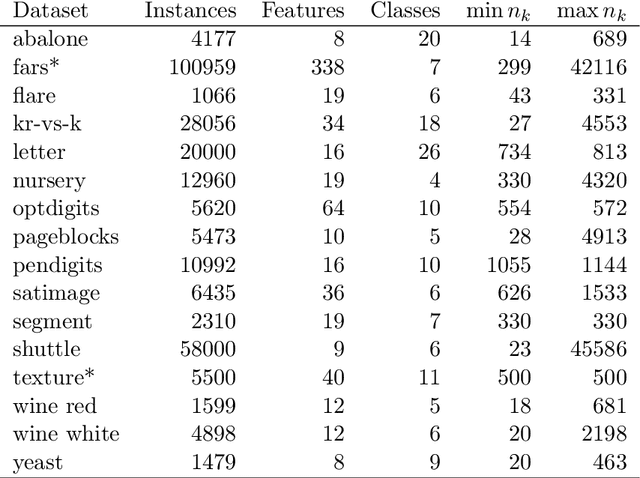
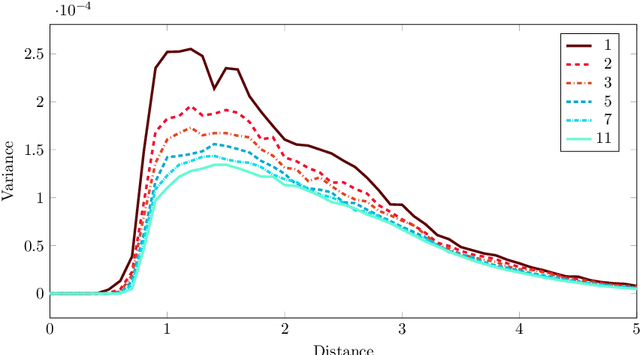
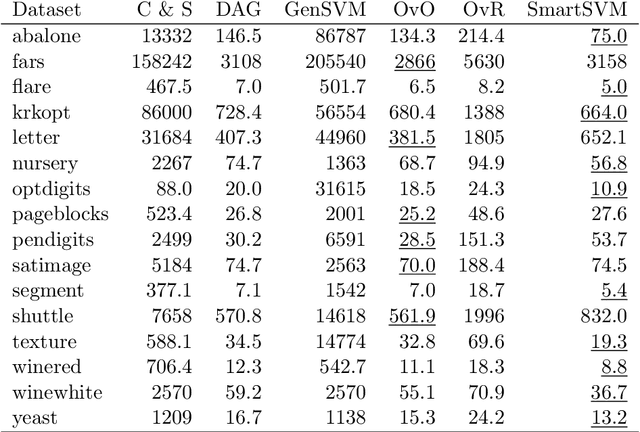
We propose a new splitting criterion for a meta-learning approach to multiclass classifier design that adaptively merges the classes into a tree-structured hierarchy of increasingly difficult binary classification problems. The classification tree is constructed from empirical estimates of the Henze-Penrose bounds on the pairwise Bayes misclassification rates that rank the binary subproblems in terms of difficulty of classification. The proposed empirical estimates of the Bayes error rate are computed from the minimal spanning tree (MST) of the samples from each pair of classes. Moreover, a meta-learning technique is presented for quantifying the one-vs-rest Bayes error rate for each individual class from a single MST on the entire dataset. Extensive simulations on benchmark datasets show that the proposed hierarchical method can often be learned much faster than competing methods, while achieving competitive accuracy.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge