Fast Design Space Exploration of Nonlinear Systems: Part I
Paper and Code
Apr 11, 2021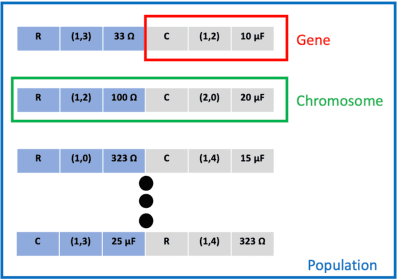
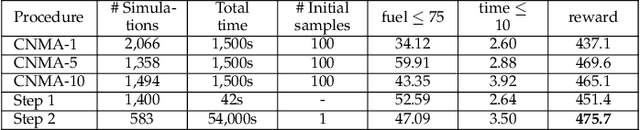
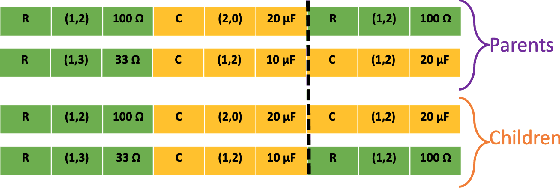
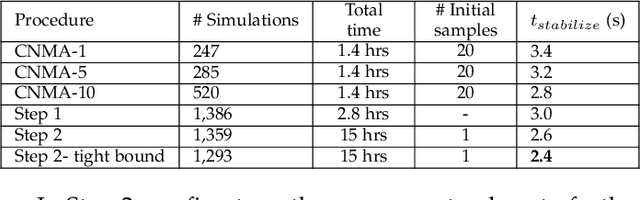
System design tools are often only available as blackboxes with complex nonlinear relationships between inputs and outputs. Blackboxes typically run in the forward direction: for a given design as input they compute an output representing system behavior. Most cannot be run in reverse to produce an input from requirements on output. Thus, finding a design satisfying a requirement is often a trial-and-error process without assurance of optimality. Finding designs concurrently satisfying multiple requirements is harder because designs satisfying individual requirements may conflict with each other. Compounding the hardness are the facts that blackbox evaluations can be expensive and sometimes fail to produce an output due to non-convergence of underlying numerical algorithms. This paper presents CNMA (Constrained optimization with Neural networks, MILP solvers and Active Learning), a new optimization method for blackboxes. It is conservative in the number of blackbox evaluations. Any designs it finds are guaranteed to satisfy all requirements. It is resilient to the failure of blackboxes to compute outputs. It tries to sample only the part of the design space relevant to solving the design problem, leveraging the power of neural networks, MILPs, and a new learning-from-failure feedback loop. The paper also presents parallel CNMA that improves the efficiency and quality of solutions over the sequential version, and tries to steer it away from local optima. CNMA's performance is evaluated for seven nonlinear design problems of 8 (2 problems), 10, 15, 36 and 60 real-valued dimensions and one with 186 binary dimensions. It is shown that CNMA improves the performance of stable, off-the-shelf implementations of Bayesian Optimization and Nelder Mead and Random Search by 1%-87% for a given fixed time and function evaluation budget. Note, that these implementations did not always return solutions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge